Showing posts with label logical games. Show all posts
Saturday, September 5, 2015
Island X
Games Reviewer
9:09 AM
brain
,
island x
,
jigsaw puzzles
,
logic
,
logical games
,
puzzle
,
puzzle games
,
puzzles online
,
riddlews online
1 comment
:
There are three categories of tribes in Island X; a Truther, who
always speaks truthfully; a Liar, who always speaks falsely; and an
Altetnator, who makes statements that are alternatively truthful and
false, albeit not necessarily in that order.
A visitor approaches three inhabitants and asks who is a Truther. They answer as follows:
A says:
1. I am a Truther
2. B is a Liar
B says:
1. I am a Alternator
2. C is a Liar
C says:
1. I am a Truther
2. A is a Liar
Determine the identity of each of the three inhabitants from the information provided in the above statements.
A visitor approaches three inhabitants and asks who is a Truther. They answer as follows:
A says:
1. I am a Truther
2. B is a Liar
B says:
1. I am a Alternator
2. C is a Liar
C says:
1. I am a Truther
2. A is a Liar
Determine the identity of each of the three inhabitants from the information provided in the above statements.
Island X Puzzle Solution
Assume that A is the Truther. If so, then B is the Liar as A's statement asserts. If so, B's second statement is false, so C is the Alternator. This implies that C's first statement is false as also his second statement that A is the Liar, so that C is the Liar which is a contradiction, so that A cannot be the Truther.Assume that B is the Truther. If so, his first statement is a direct contradiction, implying amongst other things, that B cannot be the Truther.
Assume that C is the Truther. If so, then A is the Liar in conformity with his second statement, so the remaining member B must be the Alternator. This checks out since as a Alternator, B's first statement is true while in his second statement he falsely identified C as the Liar. Both of A's statement are then clearly false, so this establishes the veracity of both the statements of C.
Consequently, (A, B, C) = (Liar, Alternator, Truther)
Friday, August 21, 2015
Switching Logic
Games Reviewer
9:04 AM
brain
,
brain teasers
,
logic
,
logical games
,
play puzzle game
,
puzzle
,
puzzles online
,
riddles online
1 comment
:

You are given plenty of time to play around with the switches in the basement, where you can put each individual switch in either its ON or OFF state.
However, you can only go upstairs once to check on the state of the bulbs!
Once you've gone upstairs and checked on the bulbs, you must be able to tell with 100% certainty which bulb is connected to which switch, without having to go down again.
How can you tell which switch is connected to each bulb?
Notes:
- You can't put a switch halfway between ON and OFF, hoping that this would make the bulb flicker like a bad neon light...
- You can't control the switches from a distance, eg with a string or whatever other form of remote control.
- You can't have anyone cooperating with you on the other floor, and that includes your dog who knows how to bark once for a 'yes' and twice for a 'no'.
Switching Logic Puzzle Solution
Turn switch #1 ON. After about five minutes or so, turn switch #1 OFF and turn switch #2 ON.Then go upstairs and check on the bulbs.
The one ON is obviously #2. The other ones are OFF, but one of them should be very hot by having been ON for five minutes. That's #1, and the remaining bulb is #3.
Sunday, August 16, 2015
Boxes, Beads, and a Blindfold
Games Reviewer
9:02 AM
beads
,
blindfold
,
boxes
,
brain
,
logic
,
logical games
,
play jigsaw puzzles
,
puzzle
,
puzzle games
,
riddles online
1 comment
:
You have been named as a traitor by the King, the punishment for this
crime is death. Although he is a cruel tyrant he gives you one last
chance at freedom. When you are finally brought before him he has this
to say to you:
"There are 100 beads, 50 black and 50 white. You will be allowed to draw one bead, whilst blindfolded of course. If it is black you will be condemned to death, if it is white you will be set free".

So far so good you think to yourself, at least I have a 50/50 chance.
"The beads will be distributed amongst four boxes by me," he continued. "You must select a box by opening it, draw one bead from it and then present the bead to the court. Thus will your fate be decided".
Upon saying this a cruel smile appears on the King's face and you suddenly break into a cold sweat as you remember that the King is both very wicked and devilishly cunning.
Assuming that the King is incredibly smart, evil, thinks that you are a stupid, uneducated peasant and wants to minimise your chance of freedom, what strategy should you employ, and what is the probability of surviving?
"There are 100 beads, 50 black and 50 white. You will be allowed to draw one bead, whilst blindfolded of course. If it is black you will be condemned to death, if it is white you will be set free".

So far so good you think to yourself, at least I have a 50/50 chance.
"The beads will be distributed amongst four boxes by me," he continued. "You must select a box by opening it, draw one bead from it and then present the bead to the court. Thus will your fate be decided".
Upon saying this a cruel smile appears on the King's face and you suddenly break into a cold sweat as you remember that the King is both very wicked and devilishly cunning.
Assuming that the King is incredibly smart, evil, thinks that you are a stupid, uneducated peasant and wants to minimise your chance of freedom, what strategy should you employ, and what is the probability of surviving?
Notes:
- The King whilst evil won't cheat.
- The trick is to work out how he plans on distributing the beads to minimise your chance of success.
- As soon as you stick your hand in one of the boxes you must draw a bead from it.
- The boxes and beads light and portable, however you are not allowed to remove them from the area.
- The King thinks you are stupid.
Boxes, Beads, and a Blindfold Puzzle Solution
The king puts 1 black bead in 3 of the 4 boxes and all the other beads (both black and white) in the fourth box.In the kings' view, you will just randomly pick a box because you are so stupid. This gives you barely 1 chance out of 8 to pick a white bead (1/4 to pick that one box containing white beads multiplied with almost 1/2 to pick a white bead out that box).
Assuming each of the four boxes are identical, by picking up each box in turn, you will be able to tell by weight or the rattling noises which one of the boxes contains the mixed beads. Picking the box with the mixed beads will mean that you have a slightly better than 50% chance of living.
Thanks to "Ben Leil" and "Kobold" for posting solutions in the forum
Thursday, August 6, 2015
U2 Gig
Games Reviewer
8:59 AM
bono
,
brain
,
brain teasers
,
gig
,
jigsaw puzzles
,
logic
,
logical games
,
play puzzle online
,
puzzle
,
puzzle games
,
U2
No comments
:

Unfortunately they only have one torch between them which must be used to cross the bridge safely and may not be thrown, only carried across the bridge.
The bridge will hold up to two band members at any time.
Each member crosses at their own pace and two members must go at the slower members pace.
Bono can cross in one minute, The Edge in two, Adam in five, and Larry in ten.
How do they make it in time?
U2 Gig Puzzle Solution
The trick is to get the two slowest people to cross at the same time. One solution is...- Bono and Edge cross the bridge for which they take 2 mins (Total time = 2)
- Then Bono comes back with the torch (Total Time = 2 + 1 = 3)
- Then Adam and Larry cross the bridge (Total time = 3 + 10 = 13)
- Then Edge comes back (Total = 13+2 = 15)
- Then both Bono and Edge cross the bridge (Time = 15+2=17)
Saturday, August 1, 2015
Duck Hunt
Games Reviewer
8:58 AM
brain
,
duck
,
duck hunt
,
hunt
,
logic
,
logical games
,
play puzzle online
,
puzzle
,
puzzle game
,
solve riddles online
1 comment
:
Tim and Tom were playing their Dad's old favourite game machine - a classic
Nintendo Entertainment System (NES). The game was, surprisingly, Duck Hunt.
Tom was at the controls, shooting innocent ducks with the lightgun.

Tim pokes Tom, and whines, "let me play." Tom looks back, and Mum is looking at them, so Tom begins to feel generous.
"Tell ya what, Tim. If you can answer a riddle about ducks, you can play. Otherwise, I get a half an hour more."
Tim, who occasionally can be a dunce, happily says "OK!".
Tom asks his question, "How many ducks do you have if you have two ducks in front of two ducks, two ducks behind two ducks, and two ducks between two ducks?"
Tim is stumped. "15?"
"Nope," says Tom.
"12?"
"Nope."
Exasperated, Tim says, "Ok, what is the answer?"
When Tom tells him, Mom goes off smiling, Tim stomps off, and Tom gets the high score on the game.
What it the least number of ducks to meet the conditions?

Tim pokes Tom, and whines, "let me play." Tom looks back, and Mum is looking at them, so Tom begins to feel generous.
"Tell ya what, Tim. If you can answer a riddle about ducks, you can play. Otherwise, I get a half an hour more."
Tim, who occasionally can be a dunce, happily says "OK!".
Tom asks his question, "How many ducks do you have if you have two ducks in front of two ducks, two ducks behind two ducks, and two ducks between two ducks?"
Tim is stumped. "15?"
"Nope," says Tom.
"12?"
"Nope."
Exasperated, Tim says, "Ok, what is the answer?"
When Tom tells him, Mom goes off smiling, Tim stomps off, and Tom gets the high score on the game.
What it the least number of ducks to meet the conditions?
Duck Hunt Puzzle Solution
Four ducks in a single row would do it.Tuesday, July 7, 2015
How Old is the Vicar?
Games Reviewer
8:51 AM
brain
,
brain teasing activity
,
logic
,
logical games
,
play puzzles online
,
puzzle
,
puzzle game
,
puzzles
,
vicar
No comments
:
There once was a choirmaster.
One day three people came in and asked to join the choir.
The choirmaster, who believes that there should be age for his choir's members, asks their ages.
To that question, one of them replied: "We can't tell you our ages, but we can tell you the following: the product of our ages is 2450, and the sum of our ages is twice your age."
The choirmaster is puzzled: "That's not enough information!"
Just then, the vicar walked in and said: "But I'm older than all of them"
The choirmaster, who knew the vicar's age, then exlaimed: "Ah! Now I know."
How old is the vicar?
One day three people came in and asked to join the choir.
The choirmaster, who believes that there should be age for his choir's members, asks their ages.
To that question, one of them replied: "We can't tell you our ages, but we can tell you the following: the product of our ages is 2450, and the sum of our ages is twice your age."
The choirmaster is puzzled: "That's not enough information!"
Just then, the vicar walked in and said: "But I'm older than all of them"
The choirmaster, who knew the vicar's age, then exlaimed: "Ah! Now I know."
How old is the vicar?
How Old is the Vicar? Puzzle Solution
The vicar is 50.The way to solve this puzzle, is to first of all write down all the possible permutations of three numbers whose product is 2450.
| Starting Numbers | Product | Sum | Choirmaster |
|---|---|---|---|
| 1, 1, 2450 | 2450 | 2452 | 1226 |
| 1, 2, 1225 | 2450 | 1228 | 614 |
| 1, 5, 490 | 2450 | 496 | 248 |
| 1, 7, 350 | 2450 | 358 | 179 |
| 1, 10, 245 | 2450 | 256 | 128 |
| 1, 14, 175 | 2450 | 190 | 95 |
| 1, 25, 98 | 2450 | 124 | 62 |
| 1, 35, 70 | 2450 | 106 | 53 |
| 1, 49, 50 | 2450 | 100 | 50 |
| 2, 5, 245 | 2450 | 252 | 126 |
| 2, 7, 175 | 2450 | 184 | 92 |
| 2, 25, 49 | 2450 | 76 | 38 |
| 2, 35, 35 | 2450 | 72 | 36 |
| 5, 5, 98 | 2450 | 108 | 54 |
| 5, 7, 70 | 2450 | 82 | 41 |
| 5, 10, 49 | 2450 | 64 | 32 |
| 5, 14, 35 | 2450 | 54 | 27 |
| 7, 7, 50 | 2450 | 64 | 32 |
| 7, 10, 35 | 2450 | 52 | 26 |
| 7, 14, 25 | 2450 | 46 | 23 |
Since the choirmaster, after being told that the product of the ages is 2450 and that the sum is twice his age, still can't work out the ages, we can deduce that there are two (or more) combinations with the same sum. Those combinations have been highlighted in the table above.
The vicar then claims to be older than all of them. The oldest of the three is 49 in the first remaining combination, and 50 in the other. The choirmaster knows the vicar's age, and after his claim, he deduces everyone's age. The only way he's able to do so is if the vicar is 50, leaving the combination 7, 7, 50 logically impossible (the vicar has to be older, that is at least 1 year older than the others), and therefore learning that the people's ages are 5, 10, and 49.
Thursday, July 2, 2015
The Maze
Games Reviewer
8:49 AM
brain
,
brain teasing activities
,
logic
,
logical games
,
maze
,
play puzzles online
,
puzzle
,
puzzle games
No comments
:

After entering the maze the first junction you come to is a 'T' intersection where you may continue to the left or the right. You decide to turn right. A short while later you come to another seemingly identical intersection, this time you turn to the left.
Hours later, after arriving at several hundred identical intersections and more or less randomly choosing left or right you eventually decide to head back (it's being some time since your last meal).
Unfortunately you can't remember the way you came and you didn't bring anything useful with you such as chalk or string.
What do you do?
The Maze Puzzle Solution
If there are only T junctions, then all you have to do to get back is take all of the side passages that you come across, as they are the T junctions that were taken from your original perspective.Effectively, every side passage you come across was a T junction that was taken earlier.
Of course, defining this the "ultimate" maze was a bit of an exaggeration on our part...
Monday, June 22, 2015
Alan and Bert
Games Reviewer
8:45 AM
alan
,
bert
,
brain
,
logic
,
logical games
,
mathematical riddle
,
puzzle
,
puzzle games
,
solve puzzles online
No comments
:
I told Alan and Bert that I had two different whole numbers in mind, each bigger
than 1, but less than 15. I told Alan the product of the two numbers and I told
Bert the sum of the two numbers. I explained to both of them what I had done.
Now both these friends are very clever. In fact Bert, who is a bit of a know it all, announced that it was impossible for either of them to work out the two numbers. On hearing that, Alan then worked what the two numbers were!

What was the sum of the two numbers?
Now both these friends are very clever. In fact Bert, who is a bit of a know it all, announced that it was impossible for either of them to work out the two numbers. On hearing that, Alan then worked what the two numbers were!

What was the sum of the two numbers?
Alan and Bert Puzzle Solution
| Starting Numbers | Sum | Product | Product can also be made using |
|---|---|---|---|
| 6, 5 | 11 | 30 | 10, 3 |
| 7, 4 | 11 | 28 | 14, 2 |
| 8, 3 | 11 | 24 | 6, 4 and 12, 2 |
| 9, 2 | 11 | 18 | 6, 3 and 9, 2 |
As mentioned in the question, he's quite clever - so he looks at the product that would appear if he used each of the four possible combinations. As shown in the table above, the product that appears can also be made from different numbers.
So, he announces that it is impossible for him or Alan to work out what the original numbers were. He seems to be on fairly safe ground.
Alan is a little bit more devious as well as being clever. Armed with this snippet of information he needs to look for a pair of numbers that give a non-unique sum and also give a non-unique product.
11 is the only non-unique sum which always gives a non-unique product. Alan is very clever and very smug.
Sunday, June 7, 2015
The Farmer's Problem
Games Reviewer
8:23 AM
brain
,
farmer
,
farmer problem
,
logic
,
logical games
,
logical puzzles
,
puzzle
,
puzzle game
1 comment
:
Farmer John had a problem. There were a group of brigands that had
taken all he had... except for three things: his prized wolf, his goat,
and a box of cabbages. They were coming after him, to get the rest.
These brigands did not like water, so John went to the Blue River, a
deep, fast river that no one could swim, and it had no bridges. He
always kept a boat there, because he liked to fish, but it was small. So
small, in fact, that he and only one of his precious things could be in
the boat at the same time.
It sounds simple, right? Ferry one item across at a time, and come back for the others? Well, if John leaves the goat with the cabbages alone on one side of the river the goat will eat the cabbages. If he leaves the wolf and the goat on one side the wolf will eat the goat. If john is there, only he can seperate the wolf from the goat and the goat from the cabbage.

How can farmer John keep his possessions safe from the brigands, without losing a single one?
It sounds simple, right? Ferry one item across at a time, and come back for the others? Well, if John leaves the goat with the cabbages alone on one side of the river the goat will eat the cabbages. If he leaves the wolf and the goat on one side the wolf will eat the goat. If john is there, only he can seperate the wolf from the goat and the goat from the cabbage.

How can farmer John keep his possessions safe from the brigands, without losing a single one?
The Farmer's Problem Puzzle Solution
There are two solutions:Solution A:
1) John takes the goat to the other side, and leaves it there.
2) He then takes the wolf to the other side.
3) He brings the goat back.
4) He takes the cabbages across, leaving them with the wolf.
5) John Comes back for the goat.
Solution B:
1) John takes the goat to the other side, and leaves it there.
2) He then takes the cabbages to the other side.
3) He brings the goat back.
4) He takes the wolf across, leaving it with the cabbages.
5) John Comes back for the goat.
Saturday, May 23, 2015
Sailor's Delight
Games Reviewer
8:11 AM
brain
,
logic
,
logic puzzles
,
logical games
,
play puzzles online
,
puzzle
,
puzzle games
,
sailor
,
web puzzles
No comments
:
10 pirates are ranked in order, first to last. After finding a
treasure chest of 100 gold coins, they are discussing how to divide up
the booty. They allow the lowest ranked sailor to divide up the coins
and then vote on his idea. If the number of pirates who like the
division is equal to or greater than the others who don't like it, then
the boss will say, "Make it So." (The proposer of the idea also has a
vote.)
Otherwise... well, being pirates their simple solution is to dump the unfortunate sailor into the deep blue sea and let the next pirate in line decide how to divide up the spoils.

How many pirates will be thrown into the sea?
Otherwise... well, being pirates their simple solution is to dump the unfortunate sailor into the deep blue sea and let the next pirate in line decide how to divide up the spoils.

How many pirates will be thrown into the sea?
Notes:
- Pirates are smart, want money, and love life, especially their own!
- This one is harder than average. If you are stuck, think of fewer pirates...
- Why would #1 ever vote for any schemes?
- Why would #2 ever vote for any schemes?
- ... hmmmm
Sailor's Delight Puzzle Solution
We asked you readers to send us a solution to this puzzle, and we kept an open mind about it.The first person with a simple, elegant, and, in our opinion, valid solution, is Saurabh Gupta, a faithful reader and avid puzzler. Here is Saurabh's solution.
How many pirates will be thrown into the sea? None. And the correct distribution is:
| Pirate with rank |
Number of coins |
|---|---|
| 1 | 0 |
| 2 | 1 |
| 3 | 0 |
| 4 | 1 |
| 5 | 0 |
| 6 | 1 |
| 7 | 0 |
| 8 | 1 |
| 9 | 0 |
| 10 | 96 |
Pirate 10 divided the coins. He will get the votes of pirates 2, 4, 6, 8, and himself. This is taking into consideration what each of the pirates will get if this plan is not passed.
Starting with a situation when there is only pirate 1. He keeps all the 100 coins for himself and live happily by passing the division with his only vote.
In case that there are two pirates, pirate 2 divides and he keeps 100 coins for himself while giving none to pirate 1. He still gets the division passed with his vote and live happily ever after.
In case there are three pirates, pirate 3 divides and gives pirate 1 a single coin and keeps the other 99 coins for himself. Pirate 1 would now vote in his favor because if he votes against, then pirate 2 would get a chance to divide and would keep all the loot for himself.
If four pirates are present, pirate 4 divides and now gives pirate 2 a single coin to gain his vote (who otherwise gets nothing if pirate 3 has a chance to divide the coins). In this case, pirates 1 and 3 get nothing.
Therefore, in a similar manner, the distribution when there is an extra pirate is achieved as follows:
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
There is, however, still some doubt about this solution. After all, it was said that pirates are smart. With this solution, based on a method of dividing the booty supposedly approved by all, it is shown that only one (the last one) is very smart, while 4 of them get only a coin, and 5 of them get nothing. This seems to be in conflict with the statement that pirates are smart. Even if the method was approved only by half of them (the ones who get at least a coin), 4 of these voters don't seem very smart if they get only one coin. Certainly, it couldn't have been a dictatorship decision taken by the leader, as he ends up empty-handed.
An alternative, to make the pirates look brighter, is that the dividing pirate actually shares the loot evenly between the pirates likely to give him a positive vote. In that case, the pirates who previously got only one coin, end up getting just as much as the lowest ranked, while the others get nothing again. This would entail the following solution:
| Pirate with rank |
Number of coins |
|---|---|
| 1 | 0 |
| 2 | 20 |
| 3 | 0 |
| 4 | 20 |
| 5 | 0 |
| 6 | 20 |
| 7 | 0 |
| 8 | 20 |
| 9 | 0 |
| 10 | 20 |
This alternative solution, however, defies a bit the mechanism of the division logic and process explained in the main solution. Perhaps, it would be fair to make a re-wording of the puzzle, stating that, although pirates are smart, the method of dividing the booty is forced on them by some external entity, and no pirate, not even the leader, can oppose to it. However, a rewording of the puzzle will NOT take place, as this is how it was presented on Brent's page, and we are going to preserve it.
Also, it might be possible that this is not the only acceptable solution, and another alternative solution might exist, that doesn't raise any doubts with the puzzle premises.
So, we are still asking you: send us your solution!
Monday, May 18, 2015
12 Balls
Games Reviewer
8:09 AM
balls
,
balls puzzle
,
brain
,
logic
,
logical games
,
play puzzle games
,
puzzle
,
stimulate brain activity
No comments
:

You have twelve balls that all weigh the same except one, which is either slightly lighter or slightly heavier. The only tool you have is a balance scale that can only tell you which side is heavier.
Using only three weighings, how can you deduce, without a shadow of a doubt, which is the odd one out, and if it is heavier or lighter than the others?
12 Balls Puzzle Solution
We found a good solution to this puzzle on the Cut The Knot website. They show a solution taken from the book Mathematical Spectrum, by Brian D. Bundy. Bundy shows two solutions: the first one requires different courses of action depending on the outcome of previous weighings, so it is not particularly elegant or easy to remember. The second solution involves a fixed course of action in all circumstances, and is the one that follows.In this method we weigh four specified balls against four other specified balls in each of the three weighings and note the result. If we observe say the left hand side of the balance, then for an individual weighing there are three possible alternatives: the left hand side is heavy (>), light (<) or equal (=) as compared with the right hand side of the balance.
Since three weighings are allowed, the number of different results that can be obtained is just the number of arrangements (with repetitions allowed) of the three symbols >, <, =, i.e. 3 3 = 27. If we use all twelve balls in the three weighings, and ensure that no particular ball appears on the same side of the balance in all three weighings, the outcomes >>>, <<<, === are not possible. We thus have only 24 possible outcomes and we shall show that it is possible to set up a one to one correspondence between these 24 outcomes and the conclusion that a particular ball among the twelve is heavy or light.
The 24 outcomes can be divided into two groups of twelve in each group. If we call the reverse of an outcome the outcome obtained by replacing > by <, < by > and leaving = unchanged, one group of twelve will be the reverses of the other group and vice versa. We can thus write the 24 outcomes in the form of two arrays, each array having three rows (the three weighings) and twelve columns (the twelve balls), so that each row contains four >'s, four <'s and four ='s. Thus we have, for example,
< = = = < < > > > < > =
= > < = > = < > > = < <
A B C D E F G H I J K L
< < < < > > > > = = = =
> = = = > > < < < > < =
= < > = < = > < < = > >
Friday, May 8, 2015
The Dog Situation
Games Reviewer
8:05 AM
brain
,
dog
,
dog situation puzzle
,
logic
,
logical games
,
play puzzle games online
,
puzzle
,
puzzle games
No comments
:

Of the eight dogs, three are cocker spaniels, three are terriers, and two are dachshunds. None of the four boys owns two dogs of the same breed. No two dogs of the same breed have the same name. Neither of Alec's dogs is named David and neither of Charlie's dogs is named Alec. No cocker spaniel is named Alec, and no terrier is named David. Bob does not own a terrier.
What are the names of the dachshunds, and who are their owners?
The Dog Situation Puzzle Solution
One of the dachshunds is owned by Bob and is named Alec, while the other is owned by Charlie and is called David.To get to the solution, let's gather all the information we're given:
1 Each boy has named his dogs after two of his brothers
2 Each boy has two doggy namesakes
3 There are 3 cocker spaniels, 3 terriers, and 2 dachshunds
4 None of the four boys owns two dogs of the same breed
5 No two dogs of the same breed have the same name
6 Neither of Alec's dogs is named David
7 Neither of Charlie's dogs is named Alec
8 No cocker spaniel is named Alec
9 No terrier is named David
10 Bob does not own a terrier
With this info, it follows that:
11 Alec's dogs are named Bob and Charlie (from 6 and 1)
12 Charlie's dogs are named Bob and David (from 7 and 1)
13 David's dogs are named Alec and Charlie (from 11, 12, 1 and 2)
14 Bob's dogs are named Alec and David (from 11, 12, 13, 1 and 2)
15 Bob's dogs are a cocker and a dachshund (from 3, 4 and 10)
16 The 3 cockers are called Bob, Charlie, and David (from 3, 5 and 8)
17 The 3 terriers are called Alec, Bob, and Charlie (from 3, 5 and 9)
18 The 2 dachshunds are called Alec and David, because the names Bob and Charlie are already taken by cockers and terriers (from 2, 3, 16 and 17)
19 Bob's dachshund must be called Alec, because there are no cockers with that name (from 14, 15, 16 and 18)
20 Bob's cocker is called David (from 14, 15, 16, 18 and 19)
21 The dachshund called David must belong to Charlie (from 12, 18 and 20)
Deductions 19 and 21 have given us the solution to the puzzle.
Sunday, May 3, 2015
Who Owns The Zebra?
Games Reviewer
8:03 AM
brain
,
logic
,
logical games
,
logical puzzles
,
puzzle
,
puzzle games
,
zebra
,
zebra puzzle
No comments
:
There are five houses.
Each house has its own unique color.
All house owners are of different nationalities.
They all have different pets.
They all drink different drinks.
They all smoke different cigarettes.
The English man lives in the red house.
The Swede has a dog.
The Dane drinks tea.
The green house is on the left side of the white house.
They drink coffee in the green house.
The man who smokes Pall Mall has birds.
In the yellow house they smoke Dunhill.
In the middle house they drink milk.
The Norwegian lives in the first house.
The man who smokes Blend lives in the house next to the house with cats.
In the house next to the house where they have a horse, they smoke Dunhill.
The man who smokes Blue Master drinks beer.
The German smokes Prince.
The Norwegian lives next to the blue house.
They drink water in the house next to the house where they smoke Blend.
So, who owns the Zebra?

Each house has its own unique color.
All house owners are of different nationalities.
They all have different pets.
They all drink different drinks.
They all smoke different cigarettes.
The English man lives in the red house.
The Swede has a dog.
The Dane drinks tea.
The green house is on the left side of the white house.
They drink coffee in the green house.
The man who smokes Pall Mall has birds.
In the yellow house they smoke Dunhill.
In the middle house they drink milk.
The Norwegian lives in the first house.
The man who smokes Blend lives in the house next to the house with cats.
In the house next to the house where they have a horse, they smoke Dunhill.
The man who smokes Blue Master drinks beer.
The German smokes Prince.
The Norwegian lives next to the blue house.
They drink water in the house next to the house where they smoke Blend.
So, who owns the Zebra?

Who Owns The Zebra? Puzzle Solution
The German owns the zebra!| #1 | #2 | #3 | #4 | #5 | |
|---|---|---|---|---|---|
| Nationality | Norwegian | Dane | English | German | Swede |
| Colour | Yellow | Blue | Red | Green | White |
| Drink | Water | Tea | Milk | Coffee | Beer |
| Cigarettes | Dunhill | Blend | Pall Mall | Prince | Blue Master |
| Pets | Cats | Horse | Birds | Zebra | Dog |
Tuesday, April 28, 2015
Socks And Shops
Games Reviewer
8:01 AM
brain
,
brain teasers
,
games online
,
logic
,
logical games
,
logical puzzle
,
puzzle
,
puzzles online
,
shops
,
socks
No comments
:

Without being able to see the colour of the socks, how could they divide them so that they both got 10 pairs of uniquely coloured socks each?
Socks And Shops Puzzle Solution
For each of the twenty pairs of socks, they unclipped it and gave one sock each.Thursday, April 23, 2015
Strawberry Ice Cream
Games Reviewer
8:00 AM
brain
,
logic
,
logical games
,
logical puzzles
,
play puzzle games
,
puzzle
,
puzzles online
,
riddles online
,
strawberry ice cream
No comments
:
A man walks into a bar, orders a drink, and starts chatting with the bartender.
After a while, he learns that the bartender has three children. "How old are your children?" he asks.
"Well," replies the bartender, "The product of their ages is 72."
The man thinks for a moment and then says, "That's not enough information."
"All right," continues the bartender. "If you go outside and look at the building number posted over the door to the bar, you'll see the sum of the ages."
The man steps outside, and after a few moments he reenters and declares, "Still not enough!"
The bartender smiles and says, "My youngest just loves strawberry ice cream."

How old are the children?
After a while, he learns that the bartender has three children. "How old are your children?" he asks.
"Well," replies the bartender, "The product of their ages is 72."
The man thinks for a moment and then says, "That's not enough information."
"All right," continues the bartender. "If you go outside and look at the building number posted over the door to the bar, you'll see the sum of the ages."
The man steps outside, and after a few moments he reenters and declares, "Still not enough!"
The bartender smiles and says, "My youngest just loves strawberry ice cream."

How old are the children?
Strawberry Ice Cream Puzzle Solution
First, determine all the ways that three ages can multiply together to get 72:- 72 1 1 (quite a feat for the bartender)
- 36 2 1
- 24 3 1
- 18 4 1
- 18 2 2
- 12 6 1
- 12 3 2
- 9 4 2
- 9 8 1
- 8 3 3
- 6 6 2
- 6 4 3
So the bartender tells him where to find the sum of the ages--the man now knows the sum even though we don't. Yet he still insists that there isn't enough info. This must mean that there are two permutations with the same sum; otherwise the man could have easily deduced the ages.
The only pair of permutations with the same sum are 8 3 3 and 6 6 2, which both add up to 14 (the bar's address). Now the bartender mentions his "youngest"--telling us that there is one child who is younger than the other two. This is impossible with 8 3 3--there are two 3 year olds. Therefore the ages of the children are 6, 6, and 2.
Pedants have objected that the problem is insoluble because there could be a youngest between two three year olds (even twins are not born exactly at the same time). However, the word "age" is frequently used to denote the number of years since birth. For example, I am the same age as my wife, even though technically she is a few months older than I am. And using the word "youngest" to mean "of lesser age" is also in keeping with common parlance. So I think the solution is fine as stated.
Monday, April 13, 2015
TV Show
Games Reviewer
7:57 AM
brain
,
brain teasers
,
logic
,
logical games
,
logical puzzle
,
play puzzles online
,
puzzle
,
puzzle game
,
show
,
TV
No comments
:

The contestant picked the first door as his guess. At that point, the host walked to the third door and opened it. The door led to no prize, which is something the host knew perfectly well. He then gave the chance to the contestant to switch and pick the second door, if he so wished, or to stick to his first choice and stay with the first door.
Did the contestant have a greater chance of winning the car, by sticking with the 1st door, or by switching to the 2nd door? Or were the chances equal?
Notes:
The contestant knew three things: first, that the host doesn't want him to win; second, that the host was going to open one of the doors; and third, that the host would never open the door picked by the contestant himself... regardless of where the prize really is.
TV Show Puzzle Solution
This puzzle isn't particularly new, but it became very well known in 1990, thanks to the person that allegedly had "the highest IQ ever recorded" -- 228, according to The Guinness Book of WorldRecords. Miss Marilyn vos Savant (yes, it was a female) wrote a solution to this puzzle on her weekly column, published in a popular magazine. This solution led to waves of mathematicians, statisticians, and professors to very heated discussions about the validity of it.The contestant, according to vos Savant, had a greater chance of winning the car by switching his pick to the 2nd door.
She claimed that by sticking to the first choice, the chances of winning were 1 out of 3, while the chances doubled to 2 out of 3 by switching choices. To convince her readers, she invited her readers to imagine 1 million doors instead of just 3. "You pick door number 1," she wrote, "and the host, who knows what's behind every door, and doesn't want you to win, opens all of the other doors, bar number 777,777. You wouldn't think twice about switching doors, right?"
Most of her readership didn't find it as obvious as she thought it was... She started receiving a lot of mail, much of it from mathematicians, who didn't agree at all. They argued that the chances were absolutely equal, whether or not the contestant switched choice.
The week after, she attempted to convince her readers of her reasoning, by creating a table where all 6 possible outcomes were considered:
| Door 1 | Door 2 | Door 3 | Outcome (sticking to door 1) |
| Car | Nothing | Nothing | Victory |
| Nothing | Car | Nothing | Loss |
| Nothing | Nothing | Car | Loss |
| Door 1 | Door 2 | Door 3 | Outcome (switching to other door) |
| Car | Nothing | Nothing | Loss |
| Nothing | Car | Nothing | Victory |
| Nothing | Nothing | Car | Victory |
The table, she explained, shows that "by switching choices you win 2 out of 3 times; on the other hand, by sticking to the first choice, you win only once out of of 3 times".
However, this wasn't enough to silence her critics. Actually, it was getting worse.
"When reality seems to cause such a conflict with good sense," wrote vos Savant, "people are left shaken." This time, she tried a different route. Let's imagine that, after the host shows that there's nothing behind one of the doors, the set becomes the landing pad for a UFO. Out of it comes a little green lady. Without her knowing which door was picked first by the contestant, she is asked to pick one of the remaining closed doors. The chances for her to find the car are 50%. "That's because she doesn't have the advantage enjoyed by the contestant, ie the host's help. If the prize is behind door 2, he will open door 3; if it is behind door 3, he will open door 2. Therefore, if you switch choice, you will win if the prize is behind door 2 or 3. YOU WIN IN EITHER CASES! If you DON'T switch, you'll win only if the car is behind door 1".
Apparently, she was absolutely right, because the mathematicians reluctantly admitted their mistake.
Thursday, March 19, 2015
Golf
Games Reviewer
7:40 AM
brain
,
brain teasers
,
golf
,
logic
,
logical games
,
logtical puzzles
,
play puzzles online
,
puzzle
,
puzzle games
No comments
:
Jack, Levi, Seth, and Robert were, not necessarily in this order, a
Stock Broker, a Musician, a Doctor, and a Lawyer. They drove, also not
necessarily in order, a Porsche, a Ferrari, a Cadillac, and a Corvette.
The Stock Broker, was remarking to no one in particular one day, while finishing up a round of golf which involved all four friends, that he found it curious that Jack and the Lawyer each wanted to buy the Corvette, but that the Musician didn't because he preferred his Porsche. After the game was over, Seth offered to buy a round of sodas for the Doctor, for the owner of the Cadillac, and for the owner of the Corvette. Levi, who was beaten by the Stock Broker, was in a bad mood, and so he declined Seth's offer and left without joining the others in the club house.
What car did each person own, and what were their respective occupations
The Stock Broker, was remarking to no one in particular one day, while finishing up a round of golf which involved all four friends, that he found it curious that Jack and the Lawyer each wanted to buy the Corvette, but that the Musician didn't because he preferred his Porsche. After the game was over, Seth offered to buy a round of sodas for the Doctor, for the owner of the Cadillac, and for the owner of the Corvette. Levi, who was beaten by the Stock Broker, was in a bad mood, and so he declined Seth's offer and left without joining the others in the club house.
What car did each person own, and what were their respective occupations
Golf Puzzle Solution
The clues given in the puzzle are:- The Stock Broker is not Levi.
- Jack is not the Lawyer; neither Jack nor the Lawyer owns the Corvette.
- The Musician owns the Porsche; therefore no one else owns the Porsche and the Musician owns no other car.
- Seth is not the owner of the Cadillac, the Corvette, nor is he the Doctor; also, the Doctor does not own either the Cadillac or the Corvette either.
- The Doctor, by elimination, must own the Ferrari; the Lawyer must own the Cadillac; the Stock Broker must own the Corvette.
- Tne Stock Broker owns the Corvette. Neither Seth nor Jack own the Corvette, so the Stock Broker must be Robert; since the Stock Broker drives the Corvette, then Robert drives the Corvette.
- The Lawyer owns the Cadillac. Seth does not own the Cadillac; therefore Seth is not the Lawyer; therefore Seth is the Musician; the Musician owns the Porsche; therefore Seth owns the Porsche.
- By elimination, Jack is the Doctor; the Doctor owns the Ferrari; therefore Jack owns the Ferrari.
- By elimination, Levi owns the Cadillac.
- Seth is the Musician and owns the Porsche.
- Levi is the Lawyer and owns the Cadillac.
- Jack is the Doctor and owns the Ferrari.
- Robert is the Stock Broker and owns the Corvette.
Saturday, March 14, 2015
Mountaineer
Games Reviewer
7:37 AM
brain
,
logic
,
logical games
,
mathematical riddles
,
mountaineer
,
play logical puzzles
,
puzzle
,
puzzle games
No comments
:
An Austrian mountaineer left Zurglatt, his village, at eight o'clock
in the morning, and started his climb towards the refuge Tirpitz, on
Gross Glossen mountain. He walked at a steady pace, without stopping,
and his increase in heart pulse rate was negligible. He reached the
refuge at three in the afternoon, i.e. seven hours since he left the
village. At the refuge he rested, admired the view, scribbled some notes
on his diary, sang three lieder, ate two sausages and drank a litre of beer. He then slipped into his sleeping bag and fell asleep.

The next morning, at eight o'clock, he started his descent, again with a steady pace, but faster, since he was travelling downhill. He reached Zurglatt at one in the afternoon, after walking for five hours.
Could there be a point along the path where the mountaineer walked, on the outbound and the return journey, exactly at the same time of day?

The next morning, at eight o'clock, he started his descent, again with a steady pace, but faster, since he was travelling downhill. He reached Zurglatt at one in the afternoon, after walking for five hours.
Could there be a point along the path where the mountaineer walked, on the outbound and the return journey, exactly at the same time of day?
Mountaineer Puzzle Solution
Of course there is. To make sure, imagine two mountaineers: one is in the village, and the other one is at the refuge. They'll both leave at eight o'clock, travel along the same path as our mountaineer, and at his same speed. At some point along the path they'll obviously meet.Sunday, February 22, 2015
Triangular Paradox
Games Reviewer
7:23 AM
brain
,
logic
,
logical games
,
logical puzzles
,
play puzzles online
,
puzzle
,
triangular paradox
,
triangular paradox puzzle
No comments
:
Consider the diagram below. Figure 1 shows four shapes. The same
four shapes have been rearranged in Figure 2. However, there is now a gap, but
none of the shapes have changed.
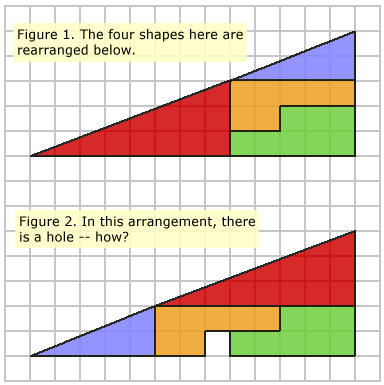 How can this be?
How can this be?

Triangular Paradox Puzzle Solution
You will have tried to calculate the areas of everything involved. The red triangle has an area of 12 squares, the blue triangle has 5 squares, the orange shape has 7, and the green shape has 8. The sum of all these parts is 12 + 5 + 7 + 8 = 32 squares.You might have thought that the large, enclosing figure was (5 × 13) / 2 = 32.5, and wondered how there is a 0.5 square discrepency.
However, this is not the case. The enclosing figures are not actually a triangles at all: the blue triangle has a gradient of 2 / 5 = 0.4, and the red triangle has a gradient of 3 / 8 = 0.375. The thick black lines aid in deceiving the eye into seeing the 'hypotenuse' as a straight line.

OK, so it's a bit of a trick. But you may note that I never said those big "triangles" were actually triangles!
Tuesday, February 17, 2015
Job Interview
Games Reviewer
7:16 AM
2 ropes puzzle
,
brain
,
job interview
,
logic
,
logical games
,
logical puzzles
,
play puzzles online
,
puzzle
No comments
:
"Come in," welcomed the interviewer.
The nervous interviewee, Tom, entered the the office, glancing back at the remaining interviewees sitting stiffly on their chairs.
"My name is Patrick," said the interviewer as he shut the door. Patrick was an elderly man with a slight stoop and a squinty eye, perhaps caused by the wearing of the monocle that now hung from his jacket pocket. "Sit down," gestured Patrick as he himself took a seat. The manner in which he spoke was somewhat strange; he seemed to group his sentences into groups of six words or so.
As Tom seated himself, he noticed that Patrick gave off a slight smell of something he could not quite identify at this moment.
"Alright," stated Patrick in his funny voice. "You must answer this question. There are two ropes. Each is one metre long. You have some matches. Each rope burns in one hour. The ropes do not burn linearly. That is, half the rope does not necessarily burn in half an hour. How do you measure out forty-five minutes?"
Tom thought for a while, and then smiled, even as that squinty eye stared hard.
Using only the matches and the two ropes, how can you measure out 45 minutes?
The nervous interviewee, Tom, entered the the office, glancing back at the remaining interviewees sitting stiffly on their chairs.
"My name is Patrick," said the interviewer as he shut the door. Patrick was an elderly man with a slight stoop and a squinty eye, perhaps caused by the wearing of the monocle that now hung from his jacket pocket. "Sit down," gestured Patrick as he himself took a seat. The manner in which he spoke was somewhat strange; he seemed to group his sentences into groups of six words or so.
As Tom seated himself, he noticed that Patrick gave off a slight smell of something he could not quite identify at this moment.
"Alright," stated Patrick in his funny voice. "You must answer this question. There are two ropes. Each is one metre long. You have some matches. Each rope burns in one hour. The ropes do not burn linearly. That is, half the rope does not necessarily burn in half an hour. How do you measure out forty-five minutes?"
Tom thought for a while, and then smiled, even as that squinty eye stared hard.
Using only the matches and the two ropes, how can you measure out 45 minutes?
Job Interview Puzzle Solution
"You set light to both ends of the rope 1 and just one end of rope 2. It will take half an hour for the two burning ends of rope 1 to meet. Then you set light to the remaining end of rope 2. The time it will take for rope 2 to finish burning will be a further 15 minutes. Hence all together, both ropes burned in this manner will take 45 minutes to burn." Tom leaned back in his chair and folded his arms.That squinty eye stared at him some more. "Very well," stated Patrick after some time. "We will let you know about the success of your application shortly." He stood and shook Tom's hand.
As Tom left the room, he grinned again. "Elderberries," he muttered to himself.
Subscribe to:
Posts
(
Atom
)







