Friday, February 27, 2015
Snake
Games Reviewer
7:30 AM
brain
,
brain teasers
,
logic
,
mathematical games
,
mathematical puzzles
,
play puzzles online
,
puzzle
,
puzzle games
,
snake
No comments
:
How are we to seat them within our only 8 remaining spaces?"
frowned the manager of the theatre. Everyone was well aware of the
problems of these eight people. They came as a group, but each person
loathed one or two of the other people and could not stand to be near
them.
The assistant manager gestured to the plan of seats remaining. "I have made eight counters to represent each of the people in this group. I have numbered them logically. Person 1 and 8 only hate 2 and 7 respectively. All the others hate the numbers on either side of them." He rubbed his chin in thought, "the only problem is how can we arrange them so that no-one is right next to anyone they hate?"

Place the counters 1 to 8 in the grey squares above such that no two consecutive counters are adjacent to one another horizontally, vertically nor diagonally.
The assistant manager gestured to the plan of seats remaining. "I have made eight counters to represent each of the people in this group. I have numbered them logically. Person 1 and 8 only hate 2 and 7 respectively. All the others hate the numbers on either side of them." He rubbed his chin in thought, "the only problem is how can we arrange them so that no-one is right next to anyone they hate?"

Place the counters 1 to 8 in the grey squares above such that no two consecutive counters are adjacent to one another horizontally, vertically nor diagonally.
Snake Puzzle Solution
Counters 1 and 8 need to be in the middle since they each have only one number that they cannot be neighbours with. Hence 7 and 2 must go in the sidewings, and the rest is trivial.| 3 | 5 | ||
| 7 | 1 | 8 | 2 |
| 4 | 6 |
Sunday, February 22, 2015
Triangular Paradox
Games Reviewer
7:23 AM
brain
,
logic
,
logical games
,
logical puzzles
,
play puzzles online
,
puzzle
,
triangular paradox
,
triangular paradox puzzle
No comments
:
Consider the diagram below. Figure 1 shows four shapes. The same
four shapes have been rearranged in Figure 2. However, there is now a gap, but
none of the shapes have changed.
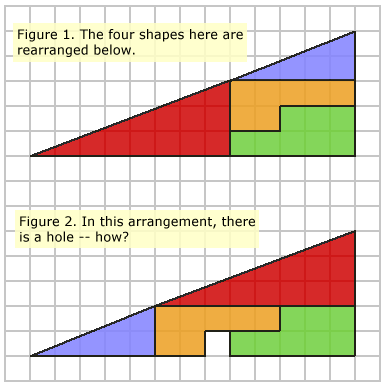 How can this be?
How can this be?

Triangular Paradox Puzzle Solution
You will have tried to calculate the areas of everything involved. The red triangle has an area of 12 squares, the blue triangle has 5 squares, the orange shape has 7, and the green shape has 8. The sum of all these parts is 12 + 5 + 7 + 8 = 32 squares.You might have thought that the large, enclosing figure was (5 × 13) / 2 = 32.5, and wondered how there is a 0.5 square discrepency.
However, this is not the case. The enclosing figures are not actually a triangles at all: the blue triangle has a gradient of 2 / 5 = 0.4, and the red triangle has a gradient of 3 / 8 = 0.375. The thick black lines aid in deceiving the eye into seeing the 'hypotenuse' as a straight line.

OK, so it's a bit of a trick. But you may note that I never said those big "triangles" were actually triangles!
Tuesday, February 17, 2015
Job Interview
Games Reviewer
7:16 AM
2 ropes puzzle
,
brain
,
job interview
,
logic
,
logical games
,
logical puzzles
,
play puzzles online
,
puzzle
No comments
:
"Come in," welcomed the interviewer.
The nervous interviewee, Tom, entered the the office, glancing back at the remaining interviewees sitting stiffly on their chairs.
"My name is Patrick," said the interviewer as he shut the door. Patrick was an elderly man with a slight stoop and a squinty eye, perhaps caused by the wearing of the monocle that now hung from his jacket pocket. "Sit down," gestured Patrick as he himself took a seat. The manner in which he spoke was somewhat strange; he seemed to group his sentences into groups of six words or so.
As Tom seated himself, he noticed that Patrick gave off a slight smell of something he could not quite identify at this moment.
"Alright," stated Patrick in his funny voice. "You must answer this question. There are two ropes. Each is one metre long. You have some matches. Each rope burns in one hour. The ropes do not burn linearly. That is, half the rope does not necessarily burn in half an hour. How do you measure out forty-five minutes?"
Tom thought for a while, and then smiled, even as that squinty eye stared hard.
Using only the matches and the two ropes, how can you measure out 45 minutes?
The nervous interviewee, Tom, entered the the office, glancing back at the remaining interviewees sitting stiffly on their chairs.
"My name is Patrick," said the interviewer as he shut the door. Patrick was an elderly man with a slight stoop and a squinty eye, perhaps caused by the wearing of the monocle that now hung from his jacket pocket. "Sit down," gestured Patrick as he himself took a seat. The manner in which he spoke was somewhat strange; he seemed to group his sentences into groups of six words or so.
As Tom seated himself, he noticed that Patrick gave off a slight smell of something he could not quite identify at this moment.
"Alright," stated Patrick in his funny voice. "You must answer this question. There are two ropes. Each is one metre long. You have some matches. Each rope burns in one hour. The ropes do not burn linearly. That is, half the rope does not necessarily burn in half an hour. How do you measure out forty-five minutes?"
Tom thought for a while, and then smiled, even as that squinty eye stared hard.
Using only the matches and the two ropes, how can you measure out 45 minutes?
Job Interview Puzzle Solution
"You set light to both ends of the rope 1 and just one end of rope 2. It will take half an hour for the two burning ends of rope 1 to meet. Then you set light to the remaining end of rope 2. The time it will take for rope 2 to finish burning will be a further 15 minutes. Hence all together, both ropes burned in this manner will take 45 minutes to burn." Tom leaned back in his chair and folded his arms.That squinty eye stared at him some more. "Very well," stated Patrick after some time. "We will let you know about the success of your application shortly." He stood and shook Tom's hand.
As Tom left the room, he grinned again. "Elderberries," he muttered to himself.
Thursday, February 12, 2015
Napoleon's Star
Games Reviewer
7:14 AM
brain
,
logic
,
logical games
,
logical puzzles
,
mathematical riddles
,
napoleon
,
napoleon star puzzle
,
puzzle
,
puzzles online
,
star
No comments
:
Napoleon had an obsession: a star. His star. He would talk about it to
everyone, and whoever would listen to him out of respect, would point at the star
in the sky. Napoleon even talked about the star during the Russian campaign, while
his troops were receding.
It seems like Talleyrand sent him the game - Napoleon's Star - on the evening of 17th June, 1815, the day before the Battle of Waterloo. It has been said that the great general spent the entire night and the following day, until sunset, trying to solve the game, without hearing the noise of the battle and without listening to his officers pleading for help. When he came out of his tent to breath some fresh air, looking tired and unshaven, but with the solution in his grasp, Waterloo had already been won by the English, and his troops were fleeing with no order or hope.

Here's the game: start from any of the ten points, marked with a letter, and follow - in a staight line - to the third point from the starting position (eg from a to g); place a coin on this third point. Then pick another point unoccupied by any coin, and again go to a third unoccupied point in a straight line (a coin on the second point doesn't matter), and place a coin on it. Repeat the procedure until you've placed nine coins.
It seems like Talleyrand sent him the game - Napoleon's Star - on the evening of 17th June, 1815, the day before the Battle of Waterloo. It has been said that the great general spent the entire night and the following day, until sunset, trying to solve the game, without hearing the noise of the battle and without listening to his officers pleading for help. When he came out of his tent to breath some fresh air, looking tired and unshaven, but with the solution in his grasp, Waterloo had already been won by the English, and his troops were fleeing with no order or hope.

Here's the game: start from any of the ten points, marked with a letter, and follow - in a staight line - to the third point from the starting position (eg from a to g); place a coin on this third point. Then pick another point unoccupied by any coin, and again go to a third unoccupied point in a straight line (a coin on the second point doesn't matter), and place a coin on it. Repeat the procedure until you've placed nine coins.
Napoleon's Star Puzzle Solution
To be able to place nine coins, it is necessary to make the 3rd point of each step equal to the start point of the previous step. For example:a-g; i-a; c-i; f-c; e-f; h-e; b-h; j-b; d-j.

With such a simple solution, it's hard to believe that Napoleon stayed in charge for so long.
Saturday, February 7, 2015
Southern Cross
Games Reviewer
7:08 AM
brain
,
logic
,
logical games
,
logical puzzles
,
mathematical puzzles
,
number puzzles
,
numers riddles
,
puzzle
,
southern cross
No comments
:
There is a missing number in the table below.
What number goes in the blank box?
| 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|
| 61 | 52 | 63 | 94 | 46 |
What number goes in the blank box?
Southern Cross Puzzle Solution
The missing number is 18. The numbers in the bottom row are the square of the numbers in the top row, but with their digits reversed.| 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|
| 61 | 52 | 63 | 94 | 46 | 18 |
Monday, February 2, 2015
Bread And Water
Games Reviewer
7:05 AM
brain
,
bread
,
bread and water puzzle
,
logic
,
logic puzzles
,
logical arcade
,
play puzzles online
,
puzzle
,
water
No comments
:

He collapsed, looked up and thought that the sun had had the better of even his eyes; he saw two bedouins walking towards him. Mirages, he thought. He shook his head and rubbed his eyes to clear it, but the bedouins were still there, getting closer. When they reached him, Alek weakly asked for water and some food, and promised he would repay them generously.
They introduced themselves as Azad and Mohammed. "Water," one of them said, "is free." As far as food was concerned, they would share with him, which consisted of bread only. Azad had three slices, and Mohammed had five. They put the slices together, split them in three equal parts, and each of them ate his portion quietly. When they finished their meal, Alek pulled out his eight golden coins, and set them before the bedouins, telling them to share them fairly. He thanked them for saving his life, promised to call them sometime, and with renewed energy continued his journey.
When the traveller was gone, the two bedouins looked at the eight golden coins for a little while, and then Mohammed moved his hand to grab five coins.
"Hold it there!" said Azad. "We will share them as good friends; four coins each!"
Mohammed was convinced he deserved five coins, but Azad would not agree, and the argument grew louder. Before the first punch was thrown, the Great Sage happened to be passing by on his camel. He enquired about the matter, which was quickly explained by the bedouins.
"Neither 5 - 3 nor 4 - 4 are fair," stated the Great Sage, before sharing his wisdom.
The bedouins got their fair share of the coins, and the Great Sage went on his way, satisfied that yet another problem had been resolved.
How much did each of the bedouins get?
Bread And Water Puzzle Solution
Each slice of bread was divided into 3 equal pieces, making a total of 24 pieces. These were then divided between the three men, 8 pieces each.Mohammed had 5 slices, and so contributed 15 pieces. He ate 8 pieces himself, so 7 were eaten by Alek.
Azad had 3 slices, which contributed 9 pieces. Azad ate 8, leaving 1 piece for Alek.
Therefore, Mohammed gave 7 pieces of bread away, and Azad only gave 1 piece. So Mohammed deserves 7 gold coins and Azad only 1. If he were smarter or less greedy, Azad should have accepted Mohammed's initial offer of 5 - 3.
Subscribe to:
Posts
(
Atom
)







