Showing posts with label logical puzzles. Show all posts
Sunday, June 7, 2015
The Farmer's Problem
Games Reviewer
8:23 AM
brain
,
farmer
,
farmer problem
,
logic
,
logical games
,
logical puzzles
,
puzzle
,
puzzle game
1 comment
:
Farmer John had a problem. There were a group of brigands that had
taken all he had... except for three things: his prized wolf, his goat,
and a box of cabbages. They were coming after him, to get the rest.
These brigands did not like water, so John went to the Blue River, a
deep, fast river that no one could swim, and it had no bridges. He
always kept a boat there, because he liked to fish, but it was small. So
small, in fact, that he and only one of his precious things could be in
the boat at the same time.
It sounds simple, right? Ferry one item across at a time, and come back for the others? Well, if John leaves the goat with the cabbages alone on one side of the river the goat will eat the cabbages. If he leaves the wolf and the goat on one side the wolf will eat the goat. If john is there, only he can seperate the wolf from the goat and the goat from the cabbage.

How can farmer John keep his possessions safe from the brigands, without losing a single one?
It sounds simple, right? Ferry one item across at a time, and come back for the others? Well, if John leaves the goat with the cabbages alone on one side of the river the goat will eat the cabbages. If he leaves the wolf and the goat on one side the wolf will eat the goat. If john is there, only he can seperate the wolf from the goat and the goat from the cabbage.

How can farmer John keep his possessions safe from the brigands, without losing a single one?
The Farmer's Problem Puzzle Solution
There are two solutions:Solution A:
1) John takes the goat to the other side, and leaves it there.
2) He then takes the wolf to the other side.
3) He brings the goat back.
4) He takes the cabbages across, leaving them with the wolf.
5) John Comes back for the goat.
Solution B:
1) John takes the goat to the other side, and leaves it there.
2) He then takes the cabbages to the other side.
3) He brings the goat back.
4) He takes the wolf across, leaving it with the cabbages.
5) John Comes back for the goat.
Thursday, May 28, 2015
The Snail And The Well
Games Reviewer
8:13 AM
brain
,
logic
,
logic games online
,
logical puzzles
,
play puzzles online
,
puzzle
,
puzzle games
,
snail
,
well
No comments
:
There was a small snail at the bottom of a thirty foot well. In
desperation to get out, the snail was only able to climb up three feet
during the daytime, and reluctantly slide back down two feet at night.
At this pace, how many days and nights will it take the snail to reach the top of the well?
At this pace, how many days and nights will it take the snail to reach the top of the well?
The Snail And The Well Puzzle Solution
After traveling 3 feet up, then sliding 2 feet down, the snail had a net gain of 1 foot per day and night. One would think, 1 foot per day and night, 30 foot deep well, 30 days and nights! But that's wrong.After 26 days and nights, the snail is 26 feet up the well. So the snail starts the 27th day at 26 feet. At the end of the 27th day, the snail has travelled to 29 feet, but during the 27th night, it slides down to 27 feet. So, on the 28th day, the snail travels 3 feet up and reaches the top of the well.
So, the final answer is 28 days and 27 nights.
Wednesday, May 13, 2015
Hugh's Horses
Games Reviewer
8:07 AM
brain
,
horses
,
logic
,
logical puzzles
,
play puzzles online
,
puzzle
,
puzzle games
,
riddle online
No comments
:
A horse breeder goes to a horse show with a certain number of horses.
The first buyer comes by and purchases half of the horses the breeder
brought plus half a horse. The second buyer comes by and purchases half
of what remains plus half a horse. The third buyer comes by and
purchases half of what remains plus half a horse. The breeder leaves,
satisfied that he has sold all the horses he brought.
All three buyers have purchased whole horses, and there is no shared ownership among them.
How many horses did the breeder bring to the show?
All three buyers have purchased whole horses, and there is no shared ownership among them.
How many horses did the breeder bring to the show?
Hugh's Horses Puzzle Solution
(0.5 + 0.5) + (0.5 + 1.5) + (0.5 + 3.5) = 7.Or here's a an algebraic solution kindy submitted by Greg Bradshaw. Thanks!
Solve for x where x is the total number of horses:
x = (.5x + .5) + (.5(.5x - .5) + .5) + (.5[.5{.5x - .5} - .5] + .5)
x = .5x + .5 + .25x - .25 + .5 + .5(.25x - .25 -.5) + .5
x = .5x + .5 + .25x + .25 + .5(.25x - .75) + .5
x = .5x + .5 + .25x + .25 + .125x - .375 + .5
x = .5x + .5 + .25x + .25 + .125x + .125
x = .875x + .875
.125x = .875
x = .875/.125
x = 7
Sunday, May 3, 2015
Who Owns The Zebra?
Games Reviewer
8:03 AM
brain
,
logic
,
logical games
,
logical puzzles
,
puzzle
,
puzzle games
,
zebra
,
zebra puzzle
No comments
:
There are five houses.
Each house has its own unique color.
All house owners are of different nationalities.
They all have different pets.
They all drink different drinks.
They all smoke different cigarettes.
The English man lives in the red house.
The Swede has a dog.
The Dane drinks tea.
The green house is on the left side of the white house.
They drink coffee in the green house.
The man who smokes Pall Mall has birds.
In the yellow house they smoke Dunhill.
In the middle house they drink milk.
The Norwegian lives in the first house.
The man who smokes Blend lives in the house next to the house with cats.
In the house next to the house where they have a horse, they smoke Dunhill.
The man who smokes Blue Master drinks beer.
The German smokes Prince.
The Norwegian lives next to the blue house.
They drink water in the house next to the house where they smoke Blend.
So, who owns the Zebra?

Each house has its own unique color.
All house owners are of different nationalities.
They all have different pets.
They all drink different drinks.
They all smoke different cigarettes.
The English man lives in the red house.
The Swede has a dog.
The Dane drinks tea.
The green house is on the left side of the white house.
They drink coffee in the green house.
The man who smokes Pall Mall has birds.
In the yellow house they smoke Dunhill.
In the middle house they drink milk.
The Norwegian lives in the first house.
The man who smokes Blend lives in the house next to the house with cats.
In the house next to the house where they have a horse, they smoke Dunhill.
The man who smokes Blue Master drinks beer.
The German smokes Prince.
The Norwegian lives next to the blue house.
They drink water in the house next to the house where they smoke Blend.
So, who owns the Zebra?

Who Owns The Zebra? Puzzle Solution
The German owns the zebra!| #1 | #2 | #3 | #4 | #5 | |
|---|---|---|---|---|---|
| Nationality | Norwegian | Dane | English | German | Swede |
| Colour | Yellow | Blue | Red | Green | White |
| Drink | Water | Tea | Milk | Coffee | Beer |
| Cigarettes | Dunhill | Blend | Pall Mall | Prince | Blue Master |
| Pets | Cats | Horse | Birds | Zebra | Dog |
Thursday, April 23, 2015
Strawberry Ice Cream
Games Reviewer
8:00 AM
brain
,
logic
,
logical games
,
logical puzzles
,
play puzzle games
,
puzzle
,
puzzles online
,
riddles online
,
strawberry ice cream
No comments
:
A man walks into a bar, orders a drink, and starts chatting with the bartender.
After a while, he learns that the bartender has three children. "How old are your children?" he asks.
"Well," replies the bartender, "The product of their ages is 72."
The man thinks for a moment and then says, "That's not enough information."
"All right," continues the bartender. "If you go outside and look at the building number posted over the door to the bar, you'll see the sum of the ages."
The man steps outside, and after a few moments he reenters and declares, "Still not enough!"
The bartender smiles and says, "My youngest just loves strawberry ice cream."

How old are the children?
After a while, he learns that the bartender has three children. "How old are your children?" he asks.
"Well," replies the bartender, "The product of their ages is 72."
The man thinks for a moment and then says, "That's not enough information."
"All right," continues the bartender. "If you go outside and look at the building number posted over the door to the bar, you'll see the sum of the ages."
The man steps outside, and after a few moments he reenters and declares, "Still not enough!"
The bartender smiles and says, "My youngest just loves strawberry ice cream."

How old are the children?
Strawberry Ice Cream Puzzle Solution
First, determine all the ways that three ages can multiply together to get 72:- 72 1 1 (quite a feat for the bartender)
- 36 2 1
- 24 3 1
- 18 4 1
- 18 2 2
- 12 6 1
- 12 3 2
- 9 4 2
- 9 8 1
- 8 3 3
- 6 6 2
- 6 4 3
So the bartender tells him where to find the sum of the ages--the man now knows the sum even though we don't. Yet he still insists that there isn't enough info. This must mean that there are two permutations with the same sum; otherwise the man could have easily deduced the ages.
The only pair of permutations with the same sum are 8 3 3 and 6 6 2, which both add up to 14 (the bar's address). Now the bartender mentions his "youngest"--telling us that there is one child who is younger than the other two. This is impossible with 8 3 3--there are two 3 year olds. Therefore the ages of the children are 6, 6, and 2.
Pedants have objected that the problem is insoluble because there could be a youngest between two three year olds (even twins are not born exactly at the same time). However, the word "age" is frequently used to denote the number of years since birth. For example, I am the same age as my wife, even though technically she is a few months older than I am. And using the word "youngest" to mean "of lesser age" is also in keeping with common parlance. So I think the solution is fine as stated.
Saturday, April 18, 2015
Hansel And Gretal
Games Reviewer
7:59 AM
brain
,
hansel and gretal
,
logic
,
logical puzzles
,
mathematical riddle
,
puzzle
,
puzzle games
,
riddle online
No comments
:
I walk in a straight line in the forest. As I walk, I leave a repeating pattern
of 1's and 0's behind me.
What is the length of the shortest pattern such that if you happen along my trail, you can determine with certainty which direction I was going?
What is the length of the shortest pattern such that if you happen along my trail, you can determine with certainty which direction I was going?
Hansel And Gretal Puzzle Solution
One solution is 010011, and is probably the shortest. In a repeating series of this pattern, we may get:
...11010011010011010011010011...
If we are to look through the sequence, we should find that we
can match the pattern 010011 but not the reverse pattern, 110010. Hence we know
which direction the person was travelling.
...11010011010011010011010011...
Friday, April 3, 2015
Trick Mules
Games Reviewer
7:53 AM
brain
,
logic
,
logical games online
,
logical puzzles
,
mules
,
play puzzle games
,
puzzle
,
trick
,
trick mules puzzle
No comments
:

Start with the three puzzle pieces arranged so that the two jockeys are correctly riding the two weary-looking mules.
Rearrange the pieces so that the mules miraculously break into a frenzied gallop!
Rearrange the pieces so that the mules miraculously break into a frenzied gallop!
Notes:
The mules do not overlap. There is a clever, but not deceptive solution to this puzzle.
Trick Mules Puzzle Solution
This ambiguous "Trick Mules Puzzle" is solved by the realisation that the mule can have two different orientations. Here the same lines and contours have two interpretations, one horizontal and one vertical.
Sunday, March 29, 2015
Camel Race
Games Reviewer
7:48 AM
brain
,
camel race
,
camel race puzzle
,
camel race riddle
,
logic
,
logical puzzles
,
puzzle
,
riddle online
No comments
:
The time had come when the father of two sons was to decide who would receive his fortune.
They both kneeled before the aged man as he spoke. "You will both race your camels to the nearest city. The owner of whichever camel arrives at the gates second will receive my fortunes."
Confused, both men rode their camels toward the city, step by step, as slow as they could. As luck would have it, the Great Sage was passing by. Seeing him, they pleaded for his wisdom.
"How might we resolve this such that it doesn't take the rest of our lives," said the first man.
"And yet it must be in a competitive manner," added the second. "Neither of us are willing to concede."
The Great Sage stroked his beard and shared his wisdom.
On hearing his advice, both men ran back to the camels and raced toward the city as fast as they could.

What was the Great Sage's suggestion?
They both kneeled before the aged man as he spoke. "You will both race your camels to the nearest city. The owner of whichever camel arrives at the gates second will receive my fortunes."
Confused, both men rode their camels toward the city, step by step, as slow as they could. As luck would have it, the Great Sage was passing by. Seeing him, they pleaded for his wisdom.
"How might we resolve this such that it doesn't take the rest of our lives," said the first man.
"And yet it must be in a competitive manner," added the second. "Neither of us are willing to concede."
The Great Sage stroked his beard and shared his wisdom.
On hearing his advice, both men ran back to the camels and raced toward the city as fast as they could.

What was the Great Sage's suggestion?
Camel Race Puzzle Solution
The Great Sage told them to swap camels. It is the second camel, not person, to reach the city gates who wins.Tuesday, March 24, 2015
Sherwood Forest
Games Reviewer
7:47 AM
brain
,
brain teasing game
,
logic
,
logical puzzles
,
puzzle
,
puzzle games online
,
sherwood forest
,
sherwood forest puzzle
No comments
:
"A three-way duel is an old tradition in these lands," said Robin
Hood, "because it is unlikely that between two champions, there
shouldn't come a third party in between, to show he is the bravest.
Miller, Allan-a-Dale, and Brother Tuck now battle like real thieves, and may the best win. Here are the crossbows, each of them with its own set of arrows. The three crossbows are all slightly different, and each set of arrows works only on the crossbow it was designed for. Unfortunately, only one set of arrows is flawless: a quarter of the set of arrows of the second crossbow is faulty, as is an incredible half of the third set. A faulty arrow is indistinguishable from a good one until it is shot. Now, go on, pick a straw, and let fate be fulfilled."
Robin Hood showed his clenched fist, from which three straws stuck out. Miller was the luckiest, having picked the longest straw, while Brother Tuck stared at his short straw with an expression of dread, for he knew full well that none of the three men would miss a target with a good arrow. "Well, Miller, here it is: the king of all crossbows. You have a 100% chance of killing your target. Allan-a-Dale, I hand you the crossbow with a few faulty arrows: with it, your chances are 75%. And there you are, Brother Tuck: the 50% crossbow. But then, a religious man like you could even duel with only your spiritual belief."
The fit monk breathed deep, and muttered, "God almighty, Robin, you want to see me dead. It is not possible to duel in these conditions."
"You are right, Brother Tuck," replied Robin Hood, after thinking for a little while. "Here is what we will do. You, Brother Tuck, will have the right to shoot first, after choosing your desired position on the field. Friends, please remember the rules: you will take position on the corners of an imaginary triangle, each of you 80 yards away from the other two. The order in which you will take turns to shoot is clockwise. On your turn, you may choose which of the other two you wish to shoot. Get ready: it is time to duel!"
Brother Tuck gulped as he chose his position, a taunting raven fluttering overhead squawking songs of doom.
 What position (A or B) did Brother Tuck choose, and which adversary
did he shoot first, in order to have the highest chance of survival?
What position (A or B) did Brother Tuck choose, and which adversary
did he shoot first, in order to have the highest chance of survival?
Miller, Allan-a-Dale, and Brother Tuck now battle like real thieves, and may the best win. Here are the crossbows, each of them with its own set of arrows. The three crossbows are all slightly different, and each set of arrows works only on the crossbow it was designed for. Unfortunately, only one set of arrows is flawless: a quarter of the set of arrows of the second crossbow is faulty, as is an incredible half of the third set. A faulty arrow is indistinguishable from a good one until it is shot. Now, go on, pick a straw, and let fate be fulfilled."
Robin Hood showed his clenched fist, from which three straws stuck out. Miller was the luckiest, having picked the longest straw, while Brother Tuck stared at his short straw with an expression of dread, for he knew full well that none of the three men would miss a target with a good arrow. "Well, Miller, here it is: the king of all crossbows. You have a 100% chance of killing your target. Allan-a-Dale, I hand you the crossbow with a few faulty arrows: with it, your chances are 75%. And there you are, Brother Tuck: the 50% crossbow. But then, a religious man like you could even duel with only your spiritual belief."
The fit monk breathed deep, and muttered, "God almighty, Robin, you want to see me dead. It is not possible to duel in these conditions."
"You are right, Brother Tuck," replied Robin Hood, after thinking for a little while. "Here is what we will do. You, Brother Tuck, will have the right to shoot first, after choosing your desired position on the field. Friends, please remember the rules: you will take position on the corners of an imaginary triangle, each of you 80 yards away from the other two. The order in which you will take turns to shoot is clockwise. On your turn, you may choose which of the other two you wish to shoot. Get ready: it is time to duel!"
Brother Tuck gulped as he chose his position, a taunting raven fluttering overhead squawking songs of doom.

Sherwood Forest Puzzle Solution
Since the order of turns was clockwise, Brother Tuck went to position B, and deliberately missed his firts shot (perhaps he should shoot the raven).Assuming that missing the first shot gives Brother Tuck the best chance that one of the dangerous adversaries gets killed from the other before becoming himself the target (obviously, both Miller and Allan-a-Dale opt to use their first turn to shoot at the most dangerous adversary), it is necessary to consider the chances of shooting from position A and the chances from position B.
By assuming position at A, and missing the first shot (as it is right in the circumstances), Brother Tuck knows that he wouldn't be Miller's target, because Allan-a-Dale is more dangerous. Allan-a-Dale would certainly be killed (Miller's crossbow has 100% chances of hitting the target). At this point, it would again be the monk's turn (with Allan not being in a condition to take his turn), who has a 50% chance of hitting the other survivor, ie Miller, and to therefore end the duel. Obviously, if the religious man misses, then he could only get on his knees and pray, because Miller's next shot would be faultless. So, by choosing position A, Brother Tuck has a 50% chance of survival.
If Brother Tuck chooses position B, and deliberately misses his first shot, the next turn would be Allan-a-Dale's, who would choose the most dangerous adversary, ie Miller. At this point, two different outcomes can happen:
1. Allan misses Miller (25% chances); at this point, Miller will use his turn to shoot Allan. Then it will be Tuck's turn, who will have one chance out of two to pick one of the good arrows (so, it's 50% chances, but it's 50% of 25%, ie 1/8).
2. Allan hits Miller (75% chances); at this point, Brother Tuck will shoot Allan, with 50% chances of success; but this is 50% of 75%, ie 3/8 which, if added to 1/8 of the first outcome, gives Tuck 4/8, ie 50% chances of survival. In case that his shot misses, Tuck would not be a sure victim of Allan's next shot, who might miss with 25% chances. This gives the monk a further 3/32 probabilities (ie 3/4 * 1/2 * 1/4).
The calculation, as shown here, could keep going on and on until the last arrow, and demonstrates that, by choosing position B, Brother Tuck has, besides the 50% chances also offered by position A, a long string of small chances (3/32, 3/256, etc), that are possible if Allan-a-Dale misses at least one (his first, and eventually the next ones) shot at the monk.
Monday, March 9, 2015
General Manoeuvres
Games Reviewer
7:35 AM
brain
,
brain teasers
,
logic
,
logical puzzles
,
manoeuvres
,
puzzle
,
puzzle games
,
puzzle games online
No comments
:
A platoon of 40 soldiers, inclusive of troopers, senior soldiers, sergeants and
commander, was standing by the bank of a river. In order to cross it, they found
only a small rubber rowing boat and a pair of paddles, belonging to two young
boys. Due to its rather restricted size, the boat can only carry either the two
boys together, or a single grown-up.
While the lieutenant - commander of the platoon - was trying to figure out the best way to organize the crossing, the radio received an urgent request: the captain wanted to know exactly how long the platoon would take to cross the river; ie how many minutes, or hours, or days were needed before the last man set his foot on the opposite bank of the river.
The lieutenant worked out that the boat, when carrying the two boys, would take 10 minutes to cross the river. One boy alone on the boat would need 5 minutes. One soldier - soldiers are not the best rowers - would take 8 minutes.
These calculations included the time taken by people to jump on board and get off the boat. After a few seconds, the officer, who had an above average IQ, sent the message with the answer to his captain.
How was the crossing organised, and how long did it take for the entire platoon to cross the river?
While the lieutenant - commander of the platoon - was trying to figure out the best way to organize the crossing, the radio received an urgent request: the captain wanted to know exactly how long the platoon would take to cross the river; ie how many minutes, or hours, or days were needed before the last man set his foot on the opposite bank of the river.
The lieutenant worked out that the boat, when carrying the two boys, would take 10 minutes to cross the river. One boy alone on the boat would need 5 minutes. One soldier - soldiers are not the best rowers - would take 8 minutes.
These calculations included the time taken by people to jump on board and get off the boat. After a few seconds, the officer, who had an above average IQ, sent the message with the answer to his captain.
How was the crossing organised, and how long did it take for the entire platoon to cross the river?
General Manoeuvres Puzzle Solution
The manoeuvre was conducted this way:- The two boys cross to the opposite bank (10 mins)
- One of them stays there while the other comes back (5 mins)
- The boy gets off the boat, a soldier jumps on board and crosses the river
(8 mins)
- The soldier gets off, and the boat returns with the other boy (5 mins)
The total time was therefore [(28 * 40) - 5] = 1115 minutes, which amounts to 18 hours and 35 minutes.
Mike Horan points out that it can be done faster if you leave both boys stranded on one side with the boat on the other. The first 39 soldiers cross at 28 minutes each (1092 minutes). You then have the two boys plus the last solider on one side. The final soldier then rows across himself, hence 1092 + 8 = 1100 minutes.
Sunday, February 22, 2015
Triangular Paradox
Games Reviewer
7:23 AM
brain
,
logic
,
logical games
,
logical puzzles
,
play puzzles online
,
puzzle
,
triangular paradox
,
triangular paradox puzzle
No comments
:
Consider the diagram below. Figure 1 shows four shapes. The same
four shapes have been rearranged in Figure 2. However, there is now a gap, but
none of the shapes have changed.
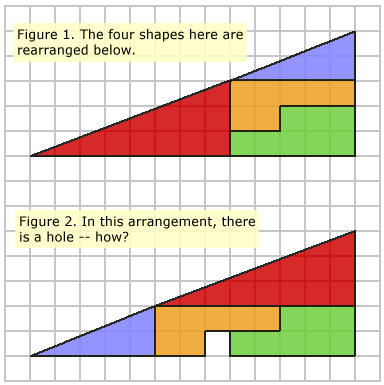 How can this be?
How can this be?

Triangular Paradox Puzzle Solution
You will have tried to calculate the areas of everything involved. The red triangle has an area of 12 squares, the blue triangle has 5 squares, the orange shape has 7, and the green shape has 8. The sum of all these parts is 12 + 5 + 7 + 8 = 32 squares.You might have thought that the large, enclosing figure was (5 × 13) / 2 = 32.5, and wondered how there is a 0.5 square discrepency.
However, this is not the case. The enclosing figures are not actually a triangles at all: the blue triangle has a gradient of 2 / 5 = 0.4, and the red triangle has a gradient of 3 / 8 = 0.375. The thick black lines aid in deceiving the eye into seeing the 'hypotenuse' as a straight line.

OK, so it's a bit of a trick. But you may note that I never said those big "triangles" were actually triangles!
Tuesday, February 17, 2015
Job Interview
Games Reviewer
7:16 AM
2 ropes puzzle
,
brain
,
job interview
,
logic
,
logical games
,
logical puzzles
,
play puzzles online
,
puzzle
No comments
:
"Come in," welcomed the interviewer.
The nervous interviewee, Tom, entered the the office, glancing back at the remaining interviewees sitting stiffly on their chairs.
"My name is Patrick," said the interviewer as he shut the door. Patrick was an elderly man with a slight stoop and a squinty eye, perhaps caused by the wearing of the monocle that now hung from his jacket pocket. "Sit down," gestured Patrick as he himself took a seat. The manner in which he spoke was somewhat strange; he seemed to group his sentences into groups of six words or so.
As Tom seated himself, he noticed that Patrick gave off a slight smell of something he could not quite identify at this moment.
"Alright," stated Patrick in his funny voice. "You must answer this question. There are two ropes. Each is one metre long. You have some matches. Each rope burns in one hour. The ropes do not burn linearly. That is, half the rope does not necessarily burn in half an hour. How do you measure out forty-five minutes?"
Tom thought for a while, and then smiled, even as that squinty eye stared hard.
Using only the matches and the two ropes, how can you measure out 45 minutes?
The nervous interviewee, Tom, entered the the office, glancing back at the remaining interviewees sitting stiffly on their chairs.
"My name is Patrick," said the interviewer as he shut the door. Patrick was an elderly man with a slight stoop and a squinty eye, perhaps caused by the wearing of the monocle that now hung from his jacket pocket. "Sit down," gestured Patrick as he himself took a seat. The manner in which he spoke was somewhat strange; he seemed to group his sentences into groups of six words or so.
As Tom seated himself, he noticed that Patrick gave off a slight smell of something he could not quite identify at this moment.
"Alright," stated Patrick in his funny voice. "You must answer this question. There are two ropes. Each is one metre long. You have some matches. Each rope burns in one hour. The ropes do not burn linearly. That is, half the rope does not necessarily burn in half an hour. How do you measure out forty-five minutes?"
Tom thought for a while, and then smiled, even as that squinty eye stared hard.
Using only the matches and the two ropes, how can you measure out 45 minutes?
Job Interview Puzzle Solution
"You set light to both ends of the rope 1 and just one end of rope 2. It will take half an hour for the two burning ends of rope 1 to meet. Then you set light to the remaining end of rope 2. The time it will take for rope 2 to finish burning will be a further 15 minutes. Hence all together, both ropes burned in this manner will take 45 minutes to burn." Tom leaned back in his chair and folded his arms.That squinty eye stared at him some more. "Very well," stated Patrick after some time. "We will let you know about the success of your application shortly." He stood and shook Tom's hand.
As Tom left the room, he grinned again. "Elderberries," he muttered to himself.
Thursday, February 12, 2015
Napoleon's Star
Games Reviewer
7:14 AM
brain
,
logic
,
logical games
,
logical puzzles
,
mathematical riddles
,
napoleon
,
napoleon star puzzle
,
puzzle
,
puzzles online
,
star
No comments
:
Napoleon had an obsession: a star. His star. He would talk about it to
everyone, and whoever would listen to him out of respect, would point at the star
in the sky. Napoleon even talked about the star during the Russian campaign, while
his troops were receding.
It seems like Talleyrand sent him the game - Napoleon's Star - on the evening of 17th June, 1815, the day before the Battle of Waterloo. It has been said that the great general spent the entire night and the following day, until sunset, trying to solve the game, without hearing the noise of the battle and without listening to his officers pleading for help. When he came out of his tent to breath some fresh air, looking tired and unshaven, but with the solution in his grasp, Waterloo had already been won by the English, and his troops were fleeing with no order or hope.

Here's the game: start from any of the ten points, marked with a letter, and follow - in a staight line - to the third point from the starting position (eg from a to g); place a coin on this third point. Then pick another point unoccupied by any coin, and again go to a third unoccupied point in a straight line (a coin on the second point doesn't matter), and place a coin on it. Repeat the procedure until you've placed nine coins.
It seems like Talleyrand sent him the game - Napoleon's Star - on the evening of 17th June, 1815, the day before the Battle of Waterloo. It has been said that the great general spent the entire night and the following day, until sunset, trying to solve the game, without hearing the noise of the battle and without listening to his officers pleading for help. When he came out of his tent to breath some fresh air, looking tired and unshaven, but with the solution in his grasp, Waterloo had already been won by the English, and his troops were fleeing with no order or hope.

Here's the game: start from any of the ten points, marked with a letter, and follow - in a staight line - to the third point from the starting position (eg from a to g); place a coin on this third point. Then pick another point unoccupied by any coin, and again go to a third unoccupied point in a straight line (a coin on the second point doesn't matter), and place a coin on it. Repeat the procedure until you've placed nine coins.
Napoleon's Star Puzzle Solution
To be able to place nine coins, it is necessary to make the 3rd point of each step equal to the start point of the previous step. For example:a-g; i-a; c-i; f-c; e-f; h-e; b-h; j-b; d-j.

With such a simple solution, it's hard to believe that Napoleon stayed in charge for so long.
Saturday, February 7, 2015
Southern Cross
Games Reviewer
7:08 AM
brain
,
logic
,
logical games
,
logical puzzles
,
mathematical puzzles
,
number puzzles
,
numers riddles
,
puzzle
,
southern cross
No comments
:
There is a missing number in the table below.
What number goes in the blank box?
| 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|
| 61 | 52 | 63 | 94 | 46 |
What number goes in the blank box?
Southern Cross Puzzle Solution
The missing number is 18. The numbers in the bottom row are the square of the numbers in the top row, but with their digits reversed.| 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|
| 61 | 52 | 63 | 94 | 46 | 18 |
Friday, January 23, 2015
Deneb
Games Reviewer
7:00 AM
brain
,
deneb
,
geometrical puzzle
,
logic
,
logical puzzles
,
play logical games
,
puzzle
,
puzzle games online
No comments
:
She was an absent minded one, forever seeing things that interest her
intellilect and hold her in thought for hours on end. On this particular
time, she saw a curious symbol, her mental processes setting
formulating a problem to solve.

Starting at any point, how can you draw the whole symbol by tracing along the lines and never tracing along the same line twice?

Starting at any point, how can you draw the whole symbol by tracing along the lines and never tracing along the same line twice?
Deneb Puzzle Solution

Sunday, January 18, 2015
Visit At The White House
Games Reviewer
6:52 AM
brain
,
brain teasers
,
logic
,
logical puzzles
,
play puzzles
,
puzzle
,
riddle online
,
white house
,
white house riddle
No comments
:
"This," started the guide, "is the Buttons Room."
The Druggar of Bongo Ghango - the chief of a large country by the River Ghango - looked around. "It's a nice room, but where are the buttons? The only ones I see are, ahem, the ones on your shirt."
"Your Highness. The buttons, which could start a nuclear armageddon in a matter of seconds, are there, behind that panel," replied the guide, while pointing at a large panel at the end of the room.
"How can that be??? Why? Anybody - a madman, for example - could come here and press those terrible buttons?"
"Your Highness, it is very safe actually: for every button there is a slot, where a magnetic card must be inserted to activate the corresponding button. No card, no button. To launch the missiles, all buttons must be activated and pressed, and only a handful of people have the magnetic cards, and each card contains a different code from all the other ones."
"But it's the same thing! Any of these persons could go completely ballistic and start a nuclear war."
"In that case, the only dangerous man is the President of the United States, as he is the only person that holds all the codes, which would allow him to press all the buttons. The other people that hold some codes are the Vice-President of the United States, the President of the Senate, the Secretary of State, the Chief of the Armed Forces, and the Dean of Harvard University. Each of these gentlemen holds an incomplete set of magnetic cards, and the distribution of the codes is such that, if the President of the United States is not available, the entire set of buttons can be activated by the Vice-President, together with anyone of the other four men. If both the President and the Vice-President of the United States are unavailable, the buttons can still be activated by any three of the other four men. Therefore, to launch the missiles, it is needed either the President, or the Vice-President plus anyone of the other four men, or any three of the other four men."
"What if someone tried to press randomly many buttons, one after the other?" asked the Chief.
"Nothing would happen with the missiles, but the room would fill up with a narcotic gas, and an alarm would alert the guards and the CIA."
"So, how many buttons are there, and how are they distributed between the Vice-President and the other four personalities?"
And that's the question we'll ask the reader: what is the minimum number of buttons, and how are they distributed?
The Druggar of Bongo Ghango - the chief of a large country by the River Ghango - looked around. "It's a nice room, but where are the buttons? The only ones I see are, ahem, the ones on your shirt."
"Your Highness. The buttons, which could start a nuclear armageddon in a matter of seconds, are there, behind that panel," replied the guide, while pointing at a large panel at the end of the room.
"How can that be??? Why? Anybody - a madman, for example - could come here and press those terrible buttons?"
"Your Highness, it is very safe actually: for every button there is a slot, where a magnetic card must be inserted to activate the corresponding button. No card, no button. To launch the missiles, all buttons must be activated and pressed, and only a handful of people have the magnetic cards, and each card contains a different code from all the other ones."
"But it's the same thing! Any of these persons could go completely ballistic and start a nuclear war."
"In that case, the only dangerous man is the President of the United States, as he is the only person that holds all the codes, which would allow him to press all the buttons. The other people that hold some codes are the Vice-President of the United States, the President of the Senate, the Secretary of State, the Chief of the Armed Forces, and the Dean of Harvard University. Each of these gentlemen holds an incomplete set of magnetic cards, and the distribution of the codes is such that, if the President of the United States is not available, the entire set of buttons can be activated by the Vice-President, together with anyone of the other four men. If both the President and the Vice-President of the United States are unavailable, the buttons can still be activated by any three of the other four men. Therefore, to launch the missiles, it is needed either the President, or the Vice-President plus anyone of the other four men, or any three of the other four men."
"What if someone tried to press randomly many buttons, one after the other?" asked the Chief.
"Nothing would happen with the missiles, but the room would fill up with a narcotic gas, and an alarm would alert the guards and the CIA."
"So, how many buttons are there, and how are they distributed between the Vice-President and the other four personalities?"
And that's the question we'll ask the reader: what is the minimum number of buttons, and how are they distributed?
Visit At The White House Puzzle Solution
There are 7 buttons. The magnetic cards, as held by the six persons,
and marked with an X, are distributed as follows:
| Person | Buttons | ||||||
|---|---|---|---|---|---|---|---|
| President | X | X | X | X | X | X | X |
| Vice President | X | X | X | X | X | X | - |
| President of Senate | X | X | X | - | - | - | X |
| Secretary of State | X | - | - | X | X | - | X |
| Chief of Armed Forces | - | X | - | X | - | X | X |
| Dean of Harvard | - | - | X | - | X | X | X |
Thursday, January 8, 2015
Frogs
Games Reviewer
6:48 AM
brain
,
frogs
,
frogs puzzle
,
logic
,
logical puzzles
,
play logical games
,
play puzzles online
,
puzzle
No comments
:

Amanda:
"I am a frog but I look like a princess."
"There are at least three frogs between the four of us."
Barbara:
"I'm a princess."
"Corinna always lies."
Corinna:
"There is only one frog here."
"I'm a frog that looks like a princess."
Deborah:
"Two of us are frogs."
"I'm a princess."
Are there any frogs? If so, what are their names
Frogs Puzzle Solution
The only frog is Amanda. The table below shows, on the left, all possible combinations of frogs (X stands for frog, - stands for non-frog), while on the right pane there is the control of the truthfullness (T for true, F for false) of each given statement, for each combination of frog population. The only combination where every girl tells one true statement and one false one, is the emphasised row. Hence, there's only one frog, and that's Amanda.| Possible Frogs | Statement | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | A | B | C | D | ||||
| - | - | - | - | F | F | T | F | F | F | F | T |
| - | - | - | X | F | F | T | F | T | F | F | F |
| - | - | X | - | F | F | T | F | T | T | F | T |
| - | - | X | X | F | F | T | T | F | T | T | F |
| - | X | - | - | F | F | F | F | T | F | F | T |
| - | X | - | X | F | F | F | F | F | F | T | F |
| - | X | X | - | F | F | F | T | F | T | T | T |
| - | X | X | X | F | T | F | T | F | T | F | F |
| X | - | - | - | T | F | T | F | T | F | F | T |
| X | - | - | X | T | F | T | F | F | F | T | F |
| X | - | X | - | T | F | T | T | F | T | T | T |
| X | - | X | X | T | T | T | T | F | T | F | F |
| X | X | - | - | T | F | F | F | F | F | T | T |
| X | X | - | X | T | T | F | F | F | F | F | F |
| X | X | X | - | T | T | F | T | F | T | F | T |
| X | X | X | X | T | T | F | T | F | T | F | F |
Saturday, January 3, 2015
Swapping Art
Games Reviewer
6:46 AM
art
,
brain
,
logic
,
logical puzzles
,
max ernst
,
max ernst art
,
puzzle
,
puzzle games
,
riddles online
,
swapping
No comments
:
"Four drawings by Max Ernst are worth as much as five sketches by Magritte,
do you agree?" asked Giorgio Parconi, an Italian art dealer. He was tired
of arguing over this.
"D'accord!" agreed Cesar Blanchard, who was the director of a Parisian art gallery.
"And we all agree that two sketches by Magritte plus one drawing by Ernst are worth as much as two paintings by Bacon. Right?"
"Bon," nodded the frenchman.
"So, I'm offering you four drawings by Ernst plus one sketch by Magritte, and in return you give me three sketches by Magritte and two paintings by Bacon. It's perfectly fair, isn't it?"
Blanchard remained silent, he had the feeling that something was wrong.
Was the Italian dealer offering a fair swap?
"D'accord!" agreed Cesar Blanchard, who was the director of a Parisian art gallery.
"And we all agree that two sketches by Magritte plus one drawing by Ernst are worth as much as two paintings by Bacon. Right?"
"Bon," nodded the frenchman.
"So, I'm offering you four drawings by Ernst plus one sketch by Magritte, and in return you give me three sketches by Magritte and two paintings by Bacon. It's perfectly fair, isn't it?"
Blanchard remained silent, he had the feeling that something was wrong.
Was the Italian dealer offering a fair swap?
Swapping Art Puzzle Solution
The swap is unfair. If we abbreviate with an E the drawings by Ernst, an M for Magritte's sketches, and a B for Bacon's paintings, we can rewrite the equations as stated by the Italian dealer as:- EEEE = MMMMM (both dealers agreed on this)
- MME = BB (again, both dealers agreed on this too)
- MMMBB = EEEEM (the French dealer wasn't sure of this)
The problem gives us 3 equations:
1. 4x = 5y
2. 2y + x = 2z
3. 3y + 2z = 4x + y
Equation 2. can be rewritten as:
4. x = -2y + 2z
Equation 3. can be rewritten as:
5. 4x = 2y + 2z
Adding equations 4. and 5. gives us:
6. 5x = 4z
Combining 1. and 6., we get:
7. 4x = 5y = (16/5)z
If we convert the offer (3.) in terms of y, we get:
8. 3y + 2(25/16)y = 5y + y
ie 3y + (25/8)y = 6y
ie 6.125y = 6y
The last equation is not absolutely true, which proves the swap is unfair.
Monday, December 29, 2014
100
Games Reviewer
6:44 AM
100
,
brain
,
logic
,
logical games online
,
logical puzzles
,
mathematical puzzles
,
mathematical riddles
,
puzzle
No comments
:
Find at least four ways of writing the number 100, each time using only one digit repeated five times.
For example: (999 / 9) - 9 = 102 (but you must get 100, not 102!!!)
Good luck!
For example: (999 / 9) - 9 = 102 (but you must get 100, not 102!!!)
Good luck!
100 Puzzle Solution
- 111 - 11 = 100
- (3 * 33) + (3 / 3) = 100
- (5 * 5 * 5) - (5 * 5) = 100
- (5 + 5 + 5 + 5) * 5 = 100
- (11 - 1) ^ ( 1 + 1) = 100 [Thanks to Steven Renich for that one!]
- ((2 * 2 * 2) + 2) ^ 2 = 100 [Thanks to David Cohen for this other one!]
- ((99 * 9) + 9) / 9 = 100 [Thanks to Taylor Lowry for this other one!]
- ((22 - 2) / 2) ^ 2 = 100 [Thanks to Karen D. Miller for this other one!]
- 6! / 6 - 6! / (6 * 6) = 100 [Thanks to Karen D. Miller for this other one!]
- 5! - 5 - 5 - 5 - 5 = 100 [Thanks to Karen D. Miller for this other one!]
- 5! - (5 + 5 + 5 + 5) = 100 [Thanks to Jim St. Clair for this other one!]
- 5 * 5 * (5 - 5 / 5) = 100 [Thanks to Rishi Mohan Sanwal for this one!]
- 4! + 4! + 4! + 4! + 4 = 100 [Thanks Karen D. Miller and Saurabh Gupta!]
- 99 + 9 ^ (9 - 9) = 100 [Thanks Gopalakrishnan Thirumurthy for this one!]
- 5! - 5 * (5 - 5 / 5) = 100 [Thanks Gopalakrishnan Thirumurthy for it!]
- (4! + 4 ^ (4 - 4)) * 4 = 100 [Thanks Gopalakrishnan Thirumurthy for it!]
- 4! * 4 + 4 - 4 + 4 = 100 [Thanks Gopalakrishnan Thirumurthy for it!]
- (4! * 4) + (4 * 4 / 4) = 100 [Thanks Gopalakrishnan Thirumurthy for it!]
- 5 * 5 * (5 - (5 - 5)!) = 100 [Thanks Gopalakrishnan Thirumurthy for it!]
- ((9 - 9) */ 9)! + 99 = 0! + 99 = 1 + 99 = 100 [Thanks to Bala Neerumalla!]
- (3 - 3)! + 33 * 3 = 100 [Thanks Bala Neerumalla for this other one!]
- (5 + 5) ^ ((5 + 5) / 5) = 100 [Thanks Bala Neerumalla for this one!]
- ((2 ^ 2) * 2 + 2) ^ 2 = 100 [Thanks Bala Neerumalla for this one!]
- (4! + ((4 - 4) */ 4)!) * 4 = 100 [Thanks Bala Neerumalla for this one!]
Glen Parnell points out that, in any solution in which the digit 2 is used, it could be replaced by 2!, whenever the 2 is not only a digit but also a number, as 2 = 2! (but of course, 22 is not equal to 22!).
Bala Neerumalla has suggested some alternative solutions using trigonometric functions Sin() and Cos():
- Sin(99 - 9) + 99 = Sin(90) + 99 = 1 + 99 = 100
- Cos((9 - 9) */ 9) + 99 = Cos(0) + 99 = 1 + 99 = 100
- Cos(3 - 3) + 33 * 3 = 100
- (4! + (Sin(4-4)*4)!)*4 = 100
- 88 + 8 + CR(8) + CR(8) = 100
- (8 + CR(8)) ^ (CR(8) * (8 / 8)) = 100
- ((CR(8) * CR(8) * CR(8)) + CR(8)) ^ CR(8) = 100
- ((8 * (8 / 8)) + CR(8)) ^ CR(8) = 100
Bala Neerumalla smartly noticed that he can produce number 100 by using a different number base than the normal base 10 (b10). The following example is in base 5 (b5):
- 444 - 44 = (4 * 5^2 + 4 * 5^1 + 4 * 5^0) - (4 * 5^1 + 4 * 5^0) = 100
- 111 - 11 = 100 [Wolfgang Solfrank pointed out that this works in any number base, thanks!]
- b16 4 ^ 4 +- 4 * (4 - 4) = 100 [Thanks to Glen Parnell for this one!]
- b16 (2 * 2 * 2 * 2) ^ 2 = 100 [Thanks to Glen Parnell for this one!]
- b8 4 * 4 * 4 +- (4 - 4) = 100 [Thanks to Glen Parnell for this one!]
- b8 (4 ^ 4) / 4 +- (4 - 4) = 100 [Thanks to Glen Parnell for this one!]
- b8 4 * 4 * 4 * (4 / 4) = 100 [Thanks to Glen Parnell for this one!]
- b8 (2 ^ (2 * 2)) * 2 * 2 = 100 [Thanks to Glen Parnell for this one!]
- b2 11 - 1 + 1 + 1 = 100 [Thanks to Glen Parnell for this one!]
- bX+1 ((X - X) */ X)! + XX = 100
- b16 ((F - F) */ F)! + FF = 100
- b12 ((B - B) */ B)! + BB = 100
- b10 ((9 - 9) */ 9)! + 99 = 100 [As already shown by Bala Neerumalla]
- b8 ((7 - 7) */ 7)! + 77 = 100
- b4 ((3 - 3) */ 3)! + 33 = 100
- b2 ((1 - 1) */ 1)! + 11 = 100
- ((L / L) + (L / L)) * L = ((50 / 50) + (50 / 50)) * 50 = 100
- (C / C) * (C / C) * C = (100 / 100) * (100 / 100) * 100 = 100
- (C / C) - (C / C) + C = (100 / 100) - (100 / 100) + 100 = 100
- CCC - CC = 300 - 200 = 100
- CC - CC + C = 200 - 200 + 100 = 100
- (L + L) * L ^ (L - L) = (50 + 50) * 50 ^ (50 - 50) = 100
- (L + L) / L ^ (L - L) = (50 + 50) / 50 ^ (50 - 50) = 100
- XX * X - X * X = 20 * 10 - 10 * 10 = 100
- (X + (X / X)) * X - X = (10 + (10 / 10)) * 10 - 10= 100
- X * X * (X ^ (X - X)) = 10 * 10 * (10 ^ (10 - 10) = 100
- X * X / (X ^ (X - X)) = 10 * 10 / (10 ^ (10 - 10) = 100
- C * C * C / C * C = 100 * 100 * 100 / 100 * 100 = 100
- (C - C) + (C - C) + C = (100 - 100) + (100 - 100) + 100 = 100
- L * (L - L) + L + L = 50 * (50 - 50) + 50 + 50 = 100
- C * (CC / C) - C = 100 * (200 / 100) - 100 = 100
- C * (C / C) + (C - C) = 100 * (100 / 100) + (100 - 100) = 100
Now, how about some solution using Roman numerals 'D' (500), or 'M' (1000)? If you find any alternative solutions, get in touch with us by email!
Easy!
Wednesday, December 24, 2014
A Law-Abiding Citizen
Games Reviewer
6:41 AM
abiding
,
brain
,
brain teasing game
,
citizen
,
law
,
logic
,
logical games
,
logical puzzles
,
puzzle
,
puzzle games
No comments
:
"Where do you think you're going with that thing?" asked the bus
driver.
"Where do you think I'm going? On this bus, of course. Why, can't I?" replied the electrician.
"No, of course you can't," said the bus driver in a very patronising way. "It is forbidden to bring any object of length, width, or height greater than one metre on any bus. That thing you're carrying is longer than one metre."
"It's got nothing to do with a ticket," screeched the driver. "You could buy a dozen tickets, and I still would not let you ride on this bus!"
Irritation grew rapidly within the electrician. "Listen! I need to take this neon light tube to a ceremony. I don't have a car. The cabbies are on strike. And it's raining. What do you expect me to do!"
"I don't know, and I don't care anyway. You ain't gonna come on this bus with that tube. End of story."
Quickly, the electrician dashed into a shop next to the bus stop and came out with a package containing the neon tube. Smugly, with all thirty-two teeth on display, he showed the package to the bus driver. "Now can I come on the bus?"
With a snort, the bus driver pulled out a folding rule and performed a precise measurement. Scowling, he waved in the smug commuter.
How did the electrician manage to pack a 1.2 metre neon tube into a package less than one metre?
"Where do you think I'm going? On this bus, of course. Why, can't I?" replied the electrician.
"No, of course you can't," said the bus driver in a very patronising way. "It is forbidden to bring any object of length, width, or height greater than one metre on any bus. That thing you're carrying is longer than one metre."
"It's got nothing to do with a ticket," screeched the driver. "You could buy a dozen tickets, and I still would not let you ride on this bus!"
Irritation grew rapidly within the electrician. "Listen! I need to take this neon light tube to a ceremony. I don't have a car. The cabbies are on strike. And it's raining. What do you expect me to do!"
"I don't know, and I don't care anyway. You ain't gonna come on this bus with that tube. End of story."
Quickly, the electrician dashed into a shop next to the bus stop and came out with a package containing the neon tube. Smugly, with all thirty-two teeth on display, he showed the package to the bus driver. "Now can I come on the bus?"
With a snort, the bus driver pulled out a folding rule and performed a precise measurement. Scowling, he waved in the smug commuter.
How did the electrician manage to pack a 1.2 metre neon tube into a package less than one metre?
A Law-Abiding Citizen Puzzle Solution
The electrician packed the tube diagonally into a flat-ish squared package, with sides of less than one metre. More precisely, the sides were about 0.85 metres long, because [squareroot(1.2² / 2) = 0.84852...]
Subscribe to:
Posts
(
Atom
)







