Showing posts with label play puzzles online. Show all posts

Tuesday, July 7, 2015

How Old is the Vicar?

Games Reviewer 8:51 AM , , , , , , , , No comments :
There once was a choirmaster.
One day three people came in and asked to join the choir.
The choirmaster, who believes that there should be age for his choir's members, asks their ages.

To that question, one of them replied: "We can't tell you our ages, but we can tell you the following: the product of our ages is 2450, and the sum of our ages is twice your age."

The choirmaster is puzzled: "That's not enough information!"

Just then, the vicar walked in and said: "But I'm older than all of them"

The choirmaster, who knew the vicar's age, then exlaimed: "Ah! Now I know."

How old is the vicar?

How Old is the Vicar? Puzzle Solution

The vicar is 50.

The way to solve this puzzle, is to first of all write down all the possible permutations of three numbers whose product is 2450.
Starting Numbers Product Sum Choirmaster
1, 1, 2450 2450 2452 1226
1, 2, 1225 2450 1228 614
1, 5, 490 2450 496 248
1, 7, 350 2450 358 179
1, 10, 245 2450 256 128
1, 14, 175 2450 190 95
1, 25, 98 2450 124 62
1, 35, 70 2450 106 53
1, 49, 50 2450 100 50
2, 5, 245 2450 252 126
2, 7, 175 2450 184 92
2, 25, 49 2450 76 38
2, 35, 35 2450 72 36
5, 5, 98 2450 108 54
5, 7, 70 2450 82 41
5, 10, 49 2450 64 32
5, 14, 35 2450 54 27
7, 7, 50 2450 64 32
7, 10, 35 2450 52 26
7, 14, 25 2450 46 23

Since the choirmaster, after being told that the product of the ages is 2450 and that the sum is twice his age, still can't work out the ages, we can deduce that there are two (or more) combinations with the same sum. Those combinations have been highlighted in the table above.

The vicar then claims to be older than all of them. The oldest of the three is 49 in the first remaining combination, and 50 in the other. The choirmaster knows the vicar's age, and after his claim, he deduces everyone's age. The only way he's able to do so is if the vicar is 50, leaving the combination 7, 7, 50 logically impossible (the vicar has to be older, that is at least 1 year older than the others), and therefore learning that the people's ages are 5, 10, and 49.

Thursday, July 2, 2015

The Maze

Games Reviewer 8:49 AM , , , , , , , No comments :
maze logic game
One day you attempt to solve the ultimate maze. A massive underground labyrinth with countless twists and turns.

After entering the maze the first junction you come to is a 'T' intersection where you may continue to the left or the right. You decide to turn right. A short while later you come to another seemingly identical intersection, this time you turn to the left.

Hours later, after arriving at several hundred identical intersections and more or less randomly choosing left or right you eventually decide to head back (it's being some time since your last meal).

Unfortunately you can't remember the way you came and you didn't bring anything useful with you such as chalk or string.

What do you do?

The Maze Puzzle Solution

If there are only T junctions, then all you have to do to get back is take all of the side passages that you come across, as they are the T junctions that were taken from your original perspective.

Effectively, every side passage you come across was a T junction that was taken earlier.

Of course, defining this the "ultimate" maze was a bit of an exaggeration on our part...

Tuesday, June 2, 2015

Loadsa Coins!

Games Reviewer 8:14 AM , , , , , , , 1 comment :
conis logical game
Laid out neatly in front of you as far as you can see are coins, coins and more coins. "That's a lot of coins," you think to yourself.

Greed sidles up to you and whispers, "Actually, there are an infinite number. And it can all be yours!"

Upon seeing your raised eyebrow, he continues. "The rules are simple. 20 of the coins are heads, the rest are tails. All you have to do is split all the coins into just two groups so that the number of heads is the same in both groups."

Seeing the obvious difficulties, you begin to protest. "But..."

"You can turn over as many coins as you like," he interrupts. "And the groups do not have to have the same number of coins in them."

"Oh ok. Can I start now?"

"Sure, you have one day to complete this task. You can start as soon as I blind you for one day."
"How can I get through it all in a day...! What do you mean blind me...!?"

Although you cannot see him, you are quite certain that he is grinning.

You cannot see. You cannot feel the difference between head nor tail. How can you accomplish this task with certainty in a single day?

Loadsa Coins! Puzzle Solution

You reach out and pick any 20 coins, and turn each of them over. The 20 coins is one group, and the remaining coins the other.

"Bugger," says Greed. "Why didn't I think of that?"

"It's so simple, yet so difficult to think of," you say. "Now can I have my eyesight back? Hello? Hello......!?"

Thursday, May 28, 2015

The Snail And The Well

Games Reviewer 8:13 AM , , , , , , , , No comments :
There was a small snail at the bottom of a thirty foot well. In desperation to get out, the snail was only able to climb up three feet during the daytime, and reluctantly slide back down two feet at night.

At this pace, how many days and nights will it take the snail to reach the top of the well?

The Snail And The Well Puzzle Solution

After traveling 3 feet up, then sliding 2 feet down, the snail had a net gain of 1 foot per day and night. One would think, 1 foot per day and night, 30 foot deep well, 30 days and nights! But that's wrong.

After 26 days and nights, the snail is 26 feet up the well. So the snail starts the 27th day at 26 feet. At the end of the 27th day, the snail has travelled to 29 feet, but during the 27th night, it slides down to 27 feet. So, on the 28th day, the snail travels 3 feet up and reaches the top of the well.

So, the final answer is 28 days and 27 nights.

Saturday, May 23, 2015

Sailor's Delight

Games Reviewer 8:11 AM , , , , , , , , No comments :
10 pirates are ranked in order, first to last. After finding a treasure chest of 100 gold coins, they are discussing how to divide up the booty. They allow the lowest ranked sailor to divide up the coins and then vote on his idea. If the number of pirates who like the division is equal to or greater than the others who don't like it, then the boss will say, "Make it So." (The proposer of the idea also has a vote.)

Otherwise... well, being pirates their simple solution is to dump the unfortunate sailor into the deep blue sea and let the next pirate in line decide how to divide up the spoils.

pirates and coins game

How many pirates will be thrown into the sea?

 

Notes:
  • Pirates are smart, want money, and love life, especially their own!
  • This one is harder than average. If you are stuck, think of fewer pirates...
  • Why would #1 ever vote for any schemes?
  • Why would #2 ever vote for any schemes?
  • ... hmmmm

Sailor's Delight Puzzle Solution

We asked you readers to send us a solution to this puzzle, and we kept an open mind about it.
The first person with a simple, elegant, and, in our opinion, valid solution, is Saurabh Gupta, a faithful reader and avid puzzler. Here is Saurabh's solution.

How many pirates will be thrown into the sea? None. And the correct distribution is:
Pirate
with rank		 Number
of coins
1 0
2 1
3 0
4 1
5 0
6 1
7 0
8 1
9 0
10 96

Pirate 10 divided the coins. He will get the votes of pirates 2, 4, 6, 8, and himself. This is taking into consideration what each of the pirates will get if this plan is not passed.

Starting with a situation when there is only pirate 1. He keeps all the 100 coins for himself and live happily by passing the division with his only vote.

In case that there are two pirates, pirate 2 divides and he keeps 100 coins for himself while giving none to pirate 1. He still gets the division passed with his vote and live happily ever after.
In case there are three pirates, pirate 3 divides and gives pirate 1 a single coin and keeps the other 99 coins for himself. Pirate 1 would now vote in his favor because if he votes against, then pirate 2 would get a chance to divide and would keep all the loot for himself.

If four pirates are present, pirate 4 divides and now gives pirate 2 a single coin to gain his vote (who otherwise gets nothing if pirate 3 has a chance to divide the coins). In this case, pirates 1 and 3 get nothing.

Therefore, in a similar manner, the distribution when there is an extra pirate is achieved as follows:

With 5 pirates,
pirate 5 divides:
Pirate
with rank		 Number
of coins
1 1
2 0
3 1
4 0
5 98
With 6 pirates,
pirate 6 divides:
Pirate
with rank		 Number
of coins
1 0
2 1
3 0
4 1
5 0
6 98
With 7 pirates,
pirate 7 divides:
Pirate
with rank		 Number
of coins
1 1
2 0
3 1
4 0
5 1
6 0
7 97
With 8 pirates,
pirate 8 divides:
Pirate
with rank		 Number
of coins
1 0
2 1
3 0
4 1
5 0
6 1
7 0
8 97
With 9 pirates,
pirate 9 divides:
Pirate
with rank		 Number
of coins
1 1
2 0
3 1
4 0
5 1
6 0
7 1
8 0
9 96
With 10 pirates,
pirate 10 divides:
Pirate
with rank		 Number
of coins
1 0
2 1
3 0
4 1
5 0
6 1
7 0
8 1
9 0
10 96
This solution holds because all pirates are rational and think through the situation. They understand that they don't get anything if the next ranked pirate gets a chance to make the division.

There is, however, still some doubt about this solution. After all, it was said that pirates are smart. With this solution, based on a method of dividing the booty supposedly approved by all, it is shown that only one (the last one) is very smart, while 4 of them get only a coin, and 5 of them get nothing. This seems to be in conflict with the statement that pirates are smart. Even if the method was approved only by half of them (the ones who get at least a coin), 4 of these voters don't seem very smart if they get only one coin. Certainly, it couldn't have been a dictatorship decision taken by the leader, as he ends up empty-handed.

An alternative, to make the pirates look brighter, is that the dividing pirate actually shares the loot evenly between the pirates likely to give him a positive vote. In that case, the pirates who previously got only one coin, end up getting just as much as the lowest ranked, while the others get nothing again. This would entail the following solution:
Pirate
with rank		 Number
of coins
1 0
2 20
3 0
4 20
5 0
6 20
7 0
8 20
9 0
10 20

This alternative solution, however, defies a bit the mechanism of the division logic and process explained in the main solution. Perhaps, it would be fair to make a re-wording of the puzzle, stating that, although pirates are smart, the method of dividing the booty is forced on them by some external entity, and no pirate, not even the leader, can oppose to it. However, a rewording of the puzzle will NOT take place, as this is how it was presented on Brent's page, and we are going to preserve it.

Also, it might be possible that this is not the only acceptable solution, and another alternative solution might exist, that doesn't raise any doubts with the puzzle premises.

So, we are still asking you: send us your solution!

Wednesday, May 13, 2015

Hugh's Horses

Games Reviewer 8:07 AM , , , , , , , No comments :
A horse breeder goes to a horse show with a certain number of horses. The first buyer comes by and purchases half of the horses the breeder brought plus half a horse. The second buyer comes by and purchases half of what remains plus half a horse. The third buyer comes by and purchases half of what remains plus half a horse. The breeder leaves, satisfied that he has sold all the horses he brought.

All three buyers have purchased whole horses, and there is no shared ownership among them.

How many horses did the breeder bring to the show?

Hugh's Horses Puzzle Solution

(0.5 + 0.5) + (0.5 + 1.5) + (0.5 + 3.5) = 7.

Or here's a an algebraic solution kindy submitted by Greg Bradshaw. Thanks!

Solve for x where x is the total number of horses:

x = (.5x + .5) + (.5(.5x - .5) + .5) + (.5[.5{.5x - .5} - .5] + .5)
x = .5x + .5 + .25x - .25 + .5 + .5(.25x - .25 -.5) + .5
x = .5x + .5 + .25x + .25 + .5(.25x - .75) + .5
x = .5x + .5 + .25x + .25 + .125x - .375 + .5
x = .5x + .5 + .25x + .25 + .125x + .125
x = .875x + .875
.125x = .875
x = .875/.125
x = 7

Monday, April 13, 2015

TV Show

Games Reviewer 7:57 AM , , , , , , , , , No comments :
3 doors puzzle
The host of the show pointed at three doors. He claimed that, behind one of the doors, a brand new sportscar was awaiting a lucky winner. The other two doors, he warned, did not lead to any prize.

The contestant picked the first door as his guess. At that point, the host walked to the third door and opened it. The door led to no prize, which is something the host knew perfectly well. He then gave the chance to the contestant to switch and pick the second door, if he so wished, or to stick to his first choice and stay with the first door.

Did the contestant have a greater chance of winning the car, by sticking with the 1st door, or by switching to the 2nd door? Or were the chances equal?

 

Notes:
The contestant knew three things: first, that the host doesn't want him to win; second, that the host was going to open one of the doors; and third, that the host would never open the door picked by the contestant himself... regardless of where the prize really is.

TV Show Puzzle Solution

This puzzle isn't particularly new, but it became very well known in 1990, thanks to the person that allegedly had "the highest IQ ever recorded" -- 228, according to The Guinness Book of WorldRecords. Miss Marilyn vos Savant (yes, it was a female) wrote a solution to this puzzle on her weekly column, published in a popular magazine. This solution led to waves of mathematicians, statisticians, and professors to very heated discussions about the validity of it.

The contestant, according to vos Savant, had a greater chance of winning the car by switching his pick to the 2nd door.

She claimed that by sticking to the first choice, the chances of winning were 1 out of 3, while the chances doubled to 2 out of 3 by switching choices. To convince her readers, she invited her readers to imagine 1 million doors instead of just 3. "You pick door number 1," she wrote, "and the host, who knows what's behind every door, and doesn't want you to win, opens all of the other doors, bar number 777,777. You wouldn't think twice about switching doors, right?"

Most of her readership didn't find it as obvious as she thought it was... She started receiving a lot of mail, much of it from mathematicians, who didn't agree at all. They argued that the chances were absolutely equal, whether or not the contestant switched choice.

The week after, she attempted to convince her readers of her reasoning, by creating a table where all 6 possible outcomes were considered:

Door 1 Door 2 Door 3 Outcome
(sticking to door 1)
Car Nothing Nothing Victory
Nothing Car Nothing Loss
Nothing Nothing Car Loss
Door 1 Door 2 Door 3 Outcome
(switching to other door)
Car Nothing Nothing Loss
Nothing Car Nothing Victory
Nothing Nothing Car Victory

The table, she explained, shows that "by switching choices you win 2 out of 3 times; on the other hand, by sticking to the first choice, you win only once out of of 3 times".

However, this wasn't enough to silence her critics. Actually, it was getting worse.

"When reality seems to cause such a conflict with good sense," wrote vos Savant, "people are left shaken." This time, she tried a different route. Let's imagine that, after the host shows that there's nothing behind one of the doors, the set becomes the landing pad for a UFO. Out of it comes a little green lady. Without her knowing which door was picked first by the contestant, she is asked to pick one of the remaining closed doors. The chances for her to find the car are 50%. "That's because she doesn't have the advantage enjoyed by the contestant, ie the host's help. If the prize is behind door 2, he will open door 3; if it is behind door 3, he will open door 2. Therefore, if you switch choice, you will win if the prize is behind door 2 or 3. YOU WIN IN EITHER CASES! If you DON'T switch, you'll win only if the car is behind door 1".

Apparently, she was absolutely right, because the mathematicians reluctantly admitted their mistake.

Wednesday, April 8, 2015

The Package

Games Reviewer 7:55 AM , , , , , , No comments :
G answered his ringing mobile phone. "G here."

"It's H. Do you have the package?"

"Yes. I have the object, in its box."

"Very good," said H. "So send the box to me using the lock I gave you last time we met."

"I'm afraid I can't," said G hestitantly.

"Why not? The locking ring on the box is more than large enough to fit a lock on."

"I seem to have um, misplaced the lock."

"You what!" snarled H. "Do you have any other locks?"

"Yes, but you don't have the keys to them. We can't risk sending an unsecured box, nor an unsecured key. Sending an unlocked lock is out of the question, because they re-lock themselves automatically after a 2 minute timeout."

"Ah, all is not lost... I have an spare lock here... How much time do we have?"

"Plenty," replied G.

"Good. There is a way…
adaugi alt

How can they get the box and the object from G to H without any security risk?

 

Notes:
  • They can't meet in person -- that would render the puzzle pointless.
  • No, G can't go and look for the misplaced lock!
  • You cannot send a key by itself or in an unlocked box.

The Package Puzzle Solution

With the object in the box, G locks it with one of his own locks. He then sends the box to H. H attaches his own lock in addition to G's and then sends it back. G removes his lock and then sends it to H again.

Thursday, March 19, 2015

Golf

Games Reviewer 7:40 AM , , , , , , , , No comments :
Jack, Levi, Seth, and Robert were, not necessarily in this order, a Stock Broker, a Musician, a Doctor, and a Lawyer. They drove, also not necessarily in order, a Porsche, a Ferrari, a Cadillac, and a Corvette.

The Stock Broker, was remarking to no one in particular one day, while finishing up a round of golf which involved all four friends, that he found it curious that Jack and the Lawyer each wanted to buy the Corvette, but that the Musician didn't because he preferred his Porsche. After the game was over, Seth offered to buy a round of sodas for the Doctor, for the owner of the Cadillac, and for the owner of the Corvette. Levi, who was beaten by the Stock Broker, was in a bad mood, and so he declined Seth's offer and left without joining the others in the club house.

What car did each person own, and what were their respective occupations

Golf Puzzle Solution

The clues given in the puzzle are:
  • The Stock Broker is not Levi.
  • Jack is not the Lawyer; neither Jack nor the Lawyer owns the Corvette.
  • The Musician owns the Porsche; therefore no one else owns the Porsche and the Musician owns no other car.
  • Seth is not the owner of the Cadillac, the Corvette, nor is he the Doctor; also, the Doctor does not own either the Cadillac or the Corvette either.
By Reasoning:
  • The Doctor, by elimination, must own the Ferrari; the Lawyer must own the Cadillac; the Stock Broker must own the Corvette.
  • Tne Stock Broker owns the Corvette. Neither Seth nor Jack own the Corvette, so the Stock Broker must be Robert; since the Stock Broker drives the Corvette, then Robert drives the Corvette.
  • The Lawyer owns the Cadillac. Seth does not own the Cadillac; therefore Seth is not the Lawyer; therefore Seth is the Musician; the Musician owns the Porsche; therefore Seth owns the Porsche.
  • By elimination, Jack is the Doctor; the Doctor owns the Ferrari; therefore Jack owns the Ferrari.
  • By elimination, Levi owns the Cadillac.
The Solution:
  • Seth is the Musician and owns the Porsche.
  • Levi is the Lawyer and owns the Cadillac.
  • Jack is the Doctor and owns the Ferrari.
  • Robert is the Stock Broker and owns the Corvette.

Friday, February 27, 2015

Snake

Games Reviewer 7:30 AM , , , , , , , , No comments :
How are we to seat them within our only 8 remaining spaces?" frowned the manager of the theatre. Everyone was well aware of the problems of these eight people. They came as a group, but each person loathed one or two of the other people and could not stand to be near them.
The assistant manager gestured to the plan of seats remaining. "I have made eight counters to represent each of the people in this group. I have numbered them logically. Person 1 and 8 only hate 2 and 7 respectively. All the others hate the numbers on either side of them." He rubbed his chin in thought, "the only problem is how can we arrange them so that no-one is right next to anyone they hate?"

Place the counters 1 to 8 in the grey squares above such that no two consecutive counters are adjacent to one another horizontally, vertically nor diagonally.

Snake Puzzle Solution

Counters 1 and 8 need to be in the middle since they each have only one number that they cannot be neighbours with. Hence 7 and 2 must go in the sidewings, and the rest is trivial.

3 5
7 1 8 2
4 6

Sunday, February 22, 2015

Triangular Paradox

Games Reviewer 7:23 AM , , , , , , , No comments :
Consider the diagram below. Figure 1 shows four shapes. The same four shapes have been rearranged in Figure 2. However, there is now a gap, but none of the shapes have changed.

triangle paradox
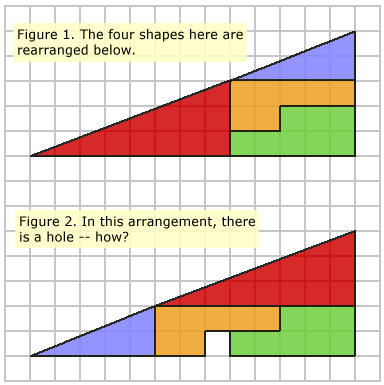How can this be?

Triangular Paradox Puzzle Solution

You will have tried to calculate the areas of everything involved. The red triangle has an area of 12 squares, the blue triangle has 5 squares, the orange shape has 7, and the green shape has 8. The sum of all these parts is 12 + 5 + 7 + 8 = 32 squares.

You might have thought that the large, enclosing figure was (5 × 13) / 2 = 32.5, and wondered how there is a 0.5 square discrepency.

However, this is not the case. The enclosing figures are not actually a triangles at all: the blue triangle has a gradient of 2 / 5 = 0.4, and the red triangle has a gradient of 3 / 8 = 0.375. The thick black lines aid in deceiving the eye into seeing the 'hypotenuse' as a straight line.
triangle paradox solution
Figure 3 shows the differing gradients with exaggerated shapes. Figure 4 shows how Figure 2's "bulge" in its hypotenuse made space for the hole.

OK, so it's a bit of a trick. But you may note that I never said those big "triangles" were actually triangles!

Tuesday, February 17, 2015

Job Interview

Games Reviewer 7:16 AM , , , , , , , No comments :
"Come in," welcomed the interviewer.

The nervous interviewee, Tom, entered the the office, glancing back at the remaining interviewees sitting stiffly on their chairs.

"My name is Patrick," said the interviewer as he shut the door. Patrick was an elderly man with a slight stoop and a squinty eye, perhaps caused by the wearing of the monocle that now hung from his jacket pocket. "Sit down," gestured Patrick as he himself took a seat. The manner in which he spoke was somewhat strange; he seemed to group his sentences into groups of six words or so.

As Tom seated himself, he noticed that Patrick gave off a slight smell of something he could not quite identify at this moment.

"Alright," stated Patrick in his funny voice. "You must answer this question. There are two ropes. Each is one metre long. You have some matches. Each rope burns in one hour. The ropes do not burn linearly. That is, half the rope does not necessarily burn in half an hour. How do you measure out forty-five minutes?"

Tom thought for a while, and then smiled, even as that squinty eye stared hard.

Using only the matches and the two ropes, how can you measure out 45 minutes?

Job Interview Puzzle Solution

"You set light to both ends of the rope 1 and just one end of rope 2. It will take half an hour for the two burning ends of rope 1 to meet. Then you set light to the remaining end of rope 2. The time it will take for rope 2 to finish burning will be a further 15 minutes. Hence all together, both ropes burned in this manner will take 45 minutes to burn." Tom leaned back in his chair and folded his arms.

That squinty eye stared at him some more. "Very well," stated Patrick after some time. "We will let you know about the success of your application shortly." He stood and shook Tom's hand.
As Tom left the room, he grinned again. "Elderberries," he muttered to himself.

Monday, February 2, 2015

Bread And Water

Games Reviewer 7:05 AM , , , , , , , , No comments :
bread and water riddle
The unforgiving heat of the desert sun was unbearable. Nearing total exhaustion, Alek the Polish traveller stumbled ever onwards through the endless expanse of sand. His camel had fled, his water reserves were long exausted, and there was not even a lizard to catch for sustenance -- not that he would have had the energy to catch it in any case. All he had left with him were the clothes he wore, eight golden coins, and his need for food and water.

He collapsed, looked up and thought that the sun had had the better of even his eyes; he saw two bedouins walking towards him. Mirages, he thought. He shook his head and rubbed his eyes to clear it, but the bedouins were still there, getting closer. When they reached him, Alek weakly asked for water and some food, and promised he would repay them generously.

They introduced themselves as Azad and Mohammed. "Water," one of them said, "is free." As far as food was concerned, they would share with him, which consisted of bread only. Azad had three slices, and Mohammed had five. They put the slices together, split them in three equal parts, and each of them ate his portion quietly. When they finished their meal, Alek pulled out his eight golden coins, and set them before the bedouins, telling them to share them fairly. He thanked them for saving his life, promised to call them sometime, and with renewed energy continued his journey.
When the traveller was gone, the two bedouins looked at the eight golden coins for a little while, and then Mohammed moved his hand to grab five coins.

"Hold it there!" said Azad. "We will share them as good friends; four coins each!"

Mohammed was convinced he deserved five coins, but Azad would not agree, and the argument grew louder. Before the first punch was thrown, the Great Sage happened to be passing by on his camel. He enquired about the matter, which was quickly explained by the bedouins.

"Neither 5 - 3 nor 4 - 4 are fair," stated the Great Sage, before sharing his wisdom.

The bedouins got their fair share of the coins, and the Great Sage went on his way, satisfied that yet another problem had been resolved.

How much did each of the bedouins get?

Bread And Water Puzzle Solution

Each slice of bread was divided into 3 equal pieces, making a total of 24 pieces. These were then divided between the three men, 8 pieces each.

Mohammed had 5 slices, and so contributed 15 pieces. He ate 8 pieces himself, so 7 were eaten by Alek.

Azad had 3 slices, which contributed 9 pieces. Azad ate 8, leaving 1 piece for Alek.

Therefore, Mohammed gave 7 pieces of bread away, and Azad only gave 1 piece. So Mohammed deserves 7 gold coins and Azad only 1. If he were smarter or less greedy, Azad should have accepted Mohammed's initial offer of 5 - 3.

Wednesday, January 28, 2015

Canopus

Games Reviewer 7:03 AM , , , , , , , No comments :
There is a number made of eleven tens of thousands, eleven thousands, eleven hundreds, and eleven units?

What is that number?

Canopus Puzzle Solution

A nice and simple sum does the trick.…
110,000 +
11,000 +
1,100 +
11 =
__________
122,111

Tuesday, January 13, 2015

Visit At The Kremlin

Games Reviewer 6:50 AM , , , , , , , , No comments :
"This," explained Colonel Nevskij to the Druggar of Bongo Ghango - chief of a large country by River Ghango - "is the Buttons Room."

"I've seen a room like this in Washington," replied the big Chief, smiling with satisfaction, "there too, you couldn't see a single button. The only ones I can see here are, uh.. hehe, the ones on your uniform, Colonel!"

"Ahah, comrade Druggar likes joking. But the buttons are here," replied the Soviet, pointing at a large panel at the end of the room, "they are behind that panel."

"A very large panel," observed the Chief, "much larger than the one at the White House: I presume there are more buttons here."

"Of course, comrade Druggar: in America, only a bunch of opportunistic capitalists has a saying in the big decisions, while here, uh, here is different: the entire Soviet community, through its representatives, takes part in the decision process of the Union."

"Any citizen could then come here and press the buttons?"

"Err, no, not exactly. If I tried to do it, the room would fill up with narcotic gas, an alarm would set off, and... Well, no need to talk about that. For each button there is a slot, into which a magnetic card must be inserted, to activate the corresponding button. Therefore, no card, no button. To launch the missiles, every button must be activated and pressed, and only a handful of comrades holds the magnetic cards, which of course, each of them has a different code from the others. The personalities holding the cards are the Secretary of the Communist Party, the President of the Praesidium, the Chief of the KGB, and five comrades, Heroes of the Soviet Union. The distribution - and here is the originality of our system - is such that the Secretary of the Party holds the complete set of codes, and so he can launch the missiles by himself; if the Secretary is not available, the missiles can be launched by the President of the Praesidium together with the Chief of the KGB, or by anyone of these two, together with any two of the five Heroes of the Union. If - Marx forbid - the Secretary, the President, and the Chief have all been victimised by an imperialistic attack, our nuclear response can be initiated by any four of the five Heroes of the Soviet Union; any four of them would be sufficient to have the entire set of magnetic cards to activate the buttons."

"So, how many buttons are there?" asked the Chief.

What is the minimum number of buttons, and how are they distributed?

Visit At The Kremlin Puzzle Solution

There are 20 buttons. This is because there are 10 combinations of Heroes in pairs of 2, and this is multiplied by 2 because these combinations have to be mapped to two different persons (the President of the Praesidium or the Chief of KGB). The magnetic cards, as held by the eight persons, and marked with an X, are distributed as follows:
Person Buttons
Secretary of Party X X X X X X X X X X X X X X X X X X X X
President of Praesidium X X X X X X X X X X X X X X X - - - - -
Chief of KGB - - - - - X X X X X X X X X X X X X X X
1st Hero X X X X - - - - - - - X X X X X X X X -
2nd Hero X X X - X X X X - - - - - - X X X X - X
3rd Hero X X - X X - - X - X X - - X - X X - X X
4th Hero X - X X X - X - X - X - X - - X - X X X
5th Hero - X X X X X - - X X - X - - - - X X X X

Thursday, January 8, 2015

Frogs

Games Reviewer 6:48 AM , , , , , , , No comments :
frogs riddle
Four ladies are facing each other. Each one of them speaks twice. One of those statements is truth, the other is a lie.

Amanda:
"I am a frog but I look like a princess."
"There are at least three frogs between the four of us."

Barbara:
"I'm a princess."
"Corinna always lies."

Corinna:
"There is only one frog here."
"I'm a frog that looks like a princess."

Deborah:
"Two of us are frogs."
"I'm a princess."

Are there any frogs? If so, what are their names

Frogs Puzzle Solution

The only frog is Amanda. The table below shows, on the left, all possible combinations of frogs (X stands for frog, - stands for non-frog), while on the right pane there is the control of the truthfullness (T for true, F for false) of each given statement, for each combination of frog population. The only combination where every girl tells one true statement and one false one, is the emphasised row. Hence, there's only one frog, and that's Amanda.
Possible Frogs Statement
A B C D A B C D
- - - - F F T F F F F T
- - - X F F T F T F F F
- - X - F F T F T T F T
- - X X F F T T F T T F
- X - - F F F F T F F T
- X - X F F F F F F T F
- X X - F F F T F T T T
- X X X F T F T F T F F
X - - - T F T F T F F T
X - - X T F T F F F T F
X - X - T F T T F T T T
X - X X T T T T F T F F
X X - - T F F F F F T T
X X - X T T F F F F F F
X X X - T T F T F T F T
X X X X T T F T F T F F

Friday, December 19, 2014

Tamerlano's Trap II

Games Reviewer 6:39 AM , , , , , , , , No comments :
Alvise Moschin, a Venetian merchant, was dragged into the Hazel Room of Samarcanda Palacethe by a pair of soldiers. Although fairly worried, Moschin felt some confidence due to his knowledge of the East. He knew, through tales heard in wine bars, what was waiting for him and how he should react. For a start, he would find himself in front of two doors guarded by two soldiers, a liar and and truth-teller. That would not be a problem.

The street-smart Venetian was thrown onto the rug before a throne. Despite his predicament, he could not contain a grin, which only widened when he saw Tamerlano enter the room and take a seat upon the throne before him.

"Get up, merchant!" barked the conqueror. "There are two doors behind you--"

"Behind one of them there's a horse, and behind the other there are crocodiles, am I right?" interrupted the merchant.

Tamerlano leaned back. "You are smart and well informed, christian," he said. "However, this time we'll have a slight variation. You will not find two guards, but one. He will be the one to whom you may ask the single question. From that, you must decide which door will lead you to certain death and which to freedom. Also, you will not know whether he always lies or always tells the truth."

With his face pale, as if he had seen a ghost, Moschin turned around and saw that between the two doors, there was indeed only one guard. The guard bore a satanic grin, his piercing eyes staring. Moschin approached the guard slowly, his mind working frantically...

What question must Alvise Moschin ask to determine which is the door to freedom?

Tamerlano's Trap II Puzzle Solution

Moschin asked the guard: "If I had asked you which door leads to freedom, which door would you have pointed me to?"

If the guard was truthful, he would have shown the right door. If he lies, he would have again shown the right door, because he would have given the merchant the opposite answer to what he would have given if he was asked a direct question.

Sunday, December 14, 2014

Tamerlano's Trap

Games Reviewer 6:34 AM , , , , , , , , No comments :
"Now be careful!" Tamerlano warned his prisoner. "You can see that in this room, there are two doors guarded by two soldiers. You can tell by their clothes that they come from two different clans. One of the doors leads to a pool of crocodiles; the other one leads to a healthy horse and a sack of gold. To determine which door leads to certain death and which leads to freedom and wealth, you may ask a single question to one of these soldiers. From that answer, you must make your decision. One more warning; one of these soldiers always tells the truth, and the other one always lies."

The prisoner, an intelligent Greek merchant, meditated for a while, bowed to the great conqueror, and with a grin on his face, approached one of the soldiers.

What question would open the door of freedom?

Tamerlano's Trap Puzzle Solution

The merchant asked one of the soldiers, it didn't matter which one: "If I had asked your colleague which door leads to freedom, which of the two doors would he have pointed me to?"

If the interrogated soldier was the one that tells the truth, he would have pointed him to the door that leads to death, because that's the door that the liar would have showed. But even if the same question was asked the liar, the same door (the one that leads to death) would have been the one pointed at, ie the door opposite the one that would have been shown by the truthful soldier.

Once obtained the answer, the merchant went to the door he was NOT pointed at, and enjoyed his freedom.

Saturday, November 29, 2014

Galactic Expedition

Games Reviewer 5:38 AM , , , , , , , , No comments :
When the scientific community predicted that the Sun would explode into a supernova in ten years time, destroying the entire Solar System, the Earthlings duly prepared for the Doomsday event. The first intergalactic spaceship was already being built, even before that prediction of doom. A sample of the human population was going to travel to the Andromeda Galaxy, where a planet in the BSC14823 solar system was believed to be able to sustain human life. It was hoped that on this planet, the human race would survive and re-establish itself as the superior being in the universe.

The person that would navigate the ship would have to rely on his/her own mathematical abilities, since obviously there could be no assistance from Earth after the explosion. The journey was predicted to last for at least 30 years, so the selection of this person was extremely tough. Only the very finest mathematical and logical mind would be able to successfully navigate the spaceship through intergalactic travel. A test to find this person was issued, and the best mathematicians of the planet competed.

spaceship puzzle

Competition was feirce, for this person would become the first hero of the new world. Of all canditates, only a young woman and a young man reached the very final stage of the selection process. The chairman of the Special Selection Board explained the final question, "There are three different integers, A, B, C, where A × B × C = 900, and A > B > C. One of you will receive either A + B or A + C, but you will not know which one of the two sums it will be. The other candidate will be given the number B. You will take turns, and the winning candidate will be the one that can tell us what the 3 numbers are."

The young man, named Wadzru, was asked to start first. "I don't know," was his answer. Then it was the young woman's turn. Her name was Zaxre, and her answer was also "I don't know." Wadzru's second turn was another "Don't know," which is the same answer given by Zaxre on her second turn. They went on answering "I don't know" for a certain number of times, until Wadzru suddenly grabbed the pen and started writing down the answer. As soon as he started writing, Zaxre cried a "YES!" and also started writing down the answer.

The selection board was confused. Wadzru did indeed answer first, but only because he was one turn ahead. Zaxre also answered correctly when it was her turn. At that moment a young mathematician entered the room. The chairman of the board called him over, and explained the mathematical problem to him. After a short pause, the man said, "If I understand the problem correctly, sir, then the two candidates must have given the correct answer on their fourth turn, that is when each of them were answering for their fourth time. At this point, I can also tell you what the three numbers are. However, there are two different answers, depending on who was given the first chance to answer: whether it was the candidate who was given number B, or the candidate who was given the sum A + B or A + C."

The board were so impressed by this latecomer that he was nominated as the commander of the expedition.

What are the two different combinations of the three numbers?

Galactic Expedition Puzzle Solution

The table below shows all possible combinations (32 of them) of three different integers, the product of which is 900. Next to each combination there is the result of the sum A+B, then the result of the sum A+C, and finally the the number B for that particular combination:
Combination # Factors A+B A+C B
1 450 * 2 * 1 452 451 2
2 300 * 3 * 1 303 301 3
3 225 * 4 * 1 229 226 4
4 180 * 5 * 1 185 181 5
5 150 * 6 * 1 156 151 6
6 100 * 9 * 1 109 101 9
7 90 * 10 * 1 100 91 10
8 75 * 12 * 1 87 76 12
9 60 * 15 * 1 75 61 15
10 50 * 18 * 1 68 51 18
11 45 * 20 * 1 65 46 20
12 36 * 25 * 1 61 37 25
13 150 * 3 * 2 153 152 3
14 90 * 5 * 2 95 92 5
15 75 * 6 * 2 81 77 6
16 50 * 9 * 2 59 52 9
17 45 * 10 * 2 55 47 10
18 30 * 15 * 2 45 32 15
19 25 * 18 * 2 43 27 18
20 75 * 4 * 3 79 78 4
21 60 * 5 * 3 65 63 5
22 50 * 6 * 3 56 53 6
23 30 * 10 * 3 40 33 10
24 25 * 12 * 3 37 28 12
25 20 * 15 * 3 35 23 15
26 45 * 5 * 4 50 49 5
27 25 * 9 * 4 34 29 9
28 30 * 6 * 5 36 35 6
29 20 * 9 * 5 29 25 9
30 18 * 10 * 5 28 23 10
31 15 * 12 * 5 27 20 12
32 15 * 10 * 6 25 21 10

If the first question was asked to the person (Wadzru) that was given A+B or A+C and he answers "don't know", that means that the number he received appears in the A+B and A+C columns more than once. On the other hand, if that number appears in those columns only once, then the solution would be found immediately, as that number would relate to only one of the 32 combinations.

Therefore the first candidate was given one of the following numbers: 65, 61, 37, 65, 29, 28, 27, 25, 23. These numbers appear more than once in columns A+B and A+C, and because of this, they do not yet allow to find the correct combination. But we can now discard, from the 32 combinations, the ones where the 9 numbers listed above are not included in columns A+B and A+C. The combinations left were then:
Combination # Factors A+B A+C B
9 60 * 15 * 1 75 61 15
11 45 * 20 * 1 65 46 20
12 36 * 25 * 1 61 37 25
19 25 * 18 * 2 43 27 18
21 60 * 5 * 3 65 63 5
24 25 * 12 * 3 37 28 12
25 20 * 15 * 3 35 23 15
27 25 * 9 * 4 34 29 9
28 30 * 6 * 5 36 35 6
29 20 * 9 * 5 29 25 9
30 18 * 10 * 5 28 23 10
31 15 * 12 * 5 27 20 12
32 15 * 10 * 6 25 21 10

The second candidate (Zaxre) followed the same reasoning, so she then knew that these were the only possible combinations left, after Wadzru gave his answer. The situation for Zaxre was the same though: if the number she was given appeared only once in column B, then the right combination would be the one containing that number; if the number appeared more than once in column B, then the solution would not yet be within reach. And this is what happened, since she answered "don't know". But the elimination of certain combinations could go on nevertheless, because after she said "don't know", combinations # 11, 12, 19, 21, 28 were automatically discarded. Then it was Wadzru's second turn, and the current situation was:
Combination # Factors A+B A+C B
9 60 * 15 * 1 75 61 15
24 25 * 12 * 3 37 28 12
25 20 * 15 * 3 35 23 15
27 25 * 9 * 4 34 29 9
29 20 * 9 * 5 29 25 9
30 18 * 10 * 5 28 23 10
31 15 * 12 * 5 27 20 12
32 15 * 10 * 6 25 21 10

At this point, the first contestant answered again "don't know", and automatically discarded combinations 9 and 31. Then the second candidate, after following, again, the logical reasoning of Wadzru, answered "don't know", therefore discarding combinations 24 and 25.The third turn started with the first contestant facing the following combinations:
Combination # Factors A+B A+C B
27 25 * 9 * 4 34 29 9
29 20 * 9 * 5 29 25 9
30 18 * 10 * 5 28 23 10
32 15 * 10 * 6 25 21 10

Wadzru, by answering "don't know" on his third turn, discarded the only combination with no alternatives, ie 30, so Zaxre was presented only with combinations 27, 29, 32; her answer "don't know" left only two combinations: 27 and 29. Then it was the first contestant again, and he was faced with the following situation:
Combination # Factors A+B A+C B
27 25 * 9 * 4 34 29 9
29 20 * 9 * 5 29 25 9

If the first contestant now answered "don't know", then the number he was given must have had to be 29; but since he was given number 25, he was able to know the correct combination requested: 20*9*5. When Zaxre saw that Wadzru had the answer, she was also able to find the solution, because she had also been able to follow the selection process. For her, it was only possible to give the answer on her 4th turn, because if Wadzru could have been able to come up with the answer on his 3rd turn (when the numbers appering just once in columns A+B and A+C were more than one), then Zaxre would not have been able to know which of the combinations contained the number given to her opponent.

If instead, the question was first asked to Zaxre, who was given number B, then after her first "don't know" it would have been possible to discard from the table (the one with all 32 combinations) combinations 1, 11, 12. After her opponent also said "don't know", the combinations to be discarded would have been 2, 3, 4, 5, 6, 7, 8, 9, 10, 13, 14, 15, 16, 17, 18, 20, 21, 22, 23 and 26, leaving the table looking like this:
Combination # Factors A+B A+C B
19 25 * 18 * 2 43 27 18
24 25 * 12 * 3 37 28 12
25 20 * 15 * 3 35 23 15
27 25 * 9 * 4 34 29 9
28 30 * 6 * 5 36 35 6
29 20 * 9 * 5 29 25 9
30 18 * 10 * 5 28 23 10
31 15 * 12 * 5 27 20 12
32 15 * 10 * 6 25 21 10

For the second turn, the "don't know" answer of the contestant answering first (Zaxre in this scenario) would have automatically discarded combinations 19, 25 and 28, and the "don't know" from her opponent would have further discarded another one: 31. For the third turn, the remaining possible combinations are: 24, 27, 29, 30 and 32. If Zaxre could not answer yet, then combination 24 would be discarded, while Wadzru's "don't know" would discard combination 30. The situation would now be:
Combination # Factors A+B A+C B
27 25 * 9 * 4 34 29 9
29 20 * 9 * 5 29 25 9
32 15 * 10 * 6 25 21 10

If Zaxre would now be able to know the solution, she would have been given, as B, number 10 (combination # 32), resulting with the product 15*10*6. But her opponent would also be able to answer then, thanks to Zaxre being able to find the solution. This scenario, like the previous one with Wadzru starting, where both opponents are able to find the solution at the same time, can only happen on the fourth turn. It's worth knowing that a fourth "don't know" from the candidates would have led to the problem being left unsolved.

Monday, November 24, 2014

Top Secret

Games Reviewer 5:36 AM , , , , , , , , No comments :
With his heart rate increasing steadily, James Bents (alias Lt-Colonel Ivanovic Zdanov, as far as the KGB were concerned) lined up behind the scientists who were walking towards the internal gate. Thanks to his forged documentation, he was able to pass through the two previous gates. He was aware that to get right inside the missile launch-pad, he would need to supply a password. He had been informed that the password changed daily. Only his extreme cool and many years of training enabled him to contain the fear.

The two scientists in front of him reached the gate, which was patrolled by machine-gun wielding soldiers. He strained to hear the voices of the people ahead of him in the queue.

"Twelve?" asked the guard.

"Six," replied the first scientist.

The first scientist strode through the gate as the second one walked to the guard.

"Six?" asked the guard.

"Three," replied the second scientist and walked through.

Relief and confidience spread through Bents; the method that drove questions and answers was trivial. He stepped forward.

"Nine?" asked the guard.

Brents hesitated for a split second. This was an unpredicted complication, but his arduous conditioning allowed the secret agent to remain calm and as sharp as a razorblade. "Four and a half," he answered without blinking.

Quite suddenly, the entire area was filled with floodlights. Alarm sirens broke the silence of the otherwise peaceful night. In a fraction of a second the Lt-Colonel realised his mistake. He tried to turn on his heels and run, but instantly felt the cold barrel of a machine-gun pressed against his neck.

What was the secret agent's fatal mistake?

Top Secret Puzzle Solution

The answers given were the the number of letters in the question. When asked "Nine?" the secret agent should have answered "Four".
Subscribe to: Posts ( Atom )

Brain Teasers Puzzles

If the solution you come up with makes the whole puzzle silly, then think again! If you got a cool puzzle that we don't, why not post it here?



Jigsaw Puzzles

Solve jigsaw puzzles online. Frame style puzzles are organized by difficulty and category.

Crosswords Puzzles

Play crossword puzzles online. Their are many different categories to choose from!

Word Search Puzzles

A nice collection of interactive word search puzzles with a milder section of printable puzzles.