Sunday, February 22, 2015
Triangular Paradox
Games Reviewer
7:23 AM
brain
,
logic
,
logical games
,
logical puzzles
,
play puzzles online
,
puzzle
,
triangular paradox
,
triangular paradox puzzle
No comments
:
Consider the diagram below. Figure 1 shows four shapes. The same
four shapes have been rearranged in Figure 2. However, there is now a gap, but
none of the shapes have changed.
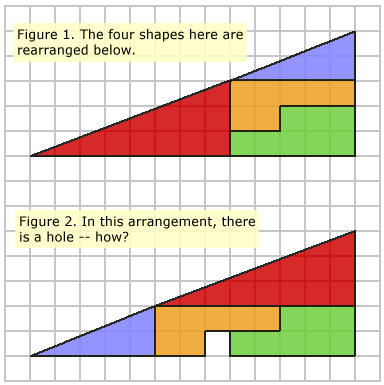 How can this be?
How can this be?

Triangular Paradox Puzzle Solution
You will have tried to calculate the areas of everything involved. The red triangle has an area of 12 squares, the blue triangle has 5 squares, the orange shape has 7, and the green shape has 8. The sum of all these parts is 12 + 5 + 7 + 8 = 32 squares.You might have thought that the large, enclosing figure was (5 × 13) / 2 = 32.5, and wondered how there is a 0.5 square discrepency.
However, this is not the case. The enclosing figures are not actually a triangles at all: the blue triangle has a gradient of 2 / 5 = 0.4, and the red triangle has a gradient of 3 / 8 = 0.375. The thick black lines aid in deceiving the eye into seeing the 'hypotenuse' as a straight line.

OK, so it's a bit of a trick. But you may note that I never said those big "triangles" were actually triangles!
Subscribe to:
Post Comments
(
Atom
)








No comments :
Post a Comment